Vẽ đồ thị của các hàm số
LG a
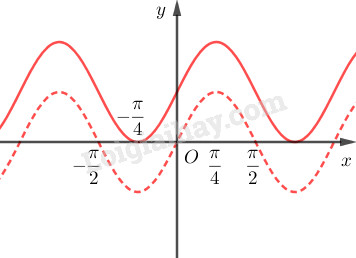
\(y=\sin 2x+1\)
Phương pháp giải:
Vẽ đồ thị hàm số \(y=\sin 2x\)
- Hàm số \(y=\sin 2x\) là hàm lẻ tuần hoàn chu kỳ \(\pi\)
- Tìm các điểm đồ thị hàm số \(y=\sin 2x\) đi qua
Vẽ đồ thị hàm số \(y=\sin 2x+1\) bằng cách tịnh tiến đồ thị hàm số \(y=\sin 2x\) song song với trục tung lên phía trên một đơn vị.
Lời giải chi tiết:
Xét hàm số \(y=\sin 2x\)
Với \(x=0\), \(y=0\); \(x=\dfrac{\pi}{4}\), \(y=1\);
\(x=-\dfrac{\pi}{4}\), \(y=-1\); \(x=\dfrac{\pi}{2}\), \(y=0\);
\(x=-\dfrac{\pi}{2}\), \(y=0\)
Khi đó đồ thị hàm số \(y=\sin 2x\) đi qua các điểm là \({\left({0;0}\right)}\); \({\left({\dfrac{\pi}{4}; 1}\right)}\); \({\left({-\dfrac{\pi}{4}; -1}\right)}\); \({\left({\dfrac{\pi}{2}; 0}\right)}\);\({\left({-\dfrac{\pi}{2}; 0}\right)}\)
Đồ thị hàm số \(y=\sin 2x+1\) thu được bằng cách tịnh tiến đồ thị hàm số \(y=\sin 2x\) song song với trục tung lên phía trên một đơn vị.
LG b
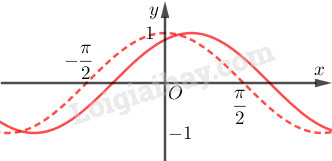
\(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\)
Phương pháp giải:
Vẽ đồ thị hàm số \(y=\cos x\)
- Hàm số \(y=\cos x\) là hàm chẵn tuần hoàn chu kỳ \(2\pi\)
- Tìm các điểm đồ thị hàm số \(y=\cos x\) đi qua
Vẽ đồ thị hàm số \(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\) bằng cách tịnh tiến đồ thị hàm số \(y=\cos x\) song song với trục hoành sang bên phải một đoạn \(\dfrac{\pi}{6}\).
Lời giải chi tiết:
Xét hàm số \(y=\cos x\)
Với \(x=0\), \(y=1\); \(x=\dfrac{\pi}{2}\), \(y=0\);
\(x=-\dfrac{\pi}{2}\), \(y=0\)
Khi đó đồ thị hàm số \(y=\sin 2x\) đi qua các điểm là \({\left({0;0}\right)}\); \({\left({\dfrac{\pi}{2}; 0}\right)}\);\({\left({-\dfrac{\pi}{2}; 0}\right)}\)
Vẽ đồ thị hàm số \(y=\cos {\left({x-\dfrac{\pi}{6}}\right)}\) bằng cách tịnh tiến đồ thị hàm số \(y=\cos x\) song song với trục hoành sang phải một đoạn bằng \(\dfrac{\pi}{6}\)