Đề bài
Trong không gian cho hai hình bình hành ABCD và A′B′C′D′ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ →BB′,→CC′,→DD′ đồng phẳng.
Phương pháp giải - Xem chi tiết
Chứng minh rằng →BB′+→DD′=→CC′ suy ra điều phải chứng minh.
Lời giải chi tiết
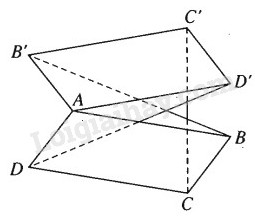
Ta có :
→BB′=→BA+→AB′,
→DD′=→DA+→AD′
Do đó →BB′+→DD′ =(→BA+→DA)+(→AB′+→AD′)
Vì →BA=→CD và →AB′+→AD′=→AC′
Nên →BB′+→DD′=(→CD+→DA)+→AC′
Vậy →BB′+→DD′=→CA+→AC′=→CC′
Hệ thức →BB′+→DD′=→CC′ biểu thị sự đồng phẳng của ba vectơ →BB′,→CC′,→DD′.

