Đề bài
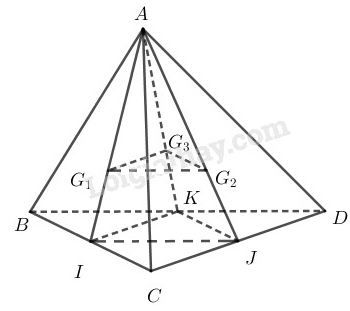
Cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng (G1G2G3)∥(BCD).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của trọng tâm trong tam giác.
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với d′ nằm trong (α) thì d song song với (α).
\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )
Sử dụng tính chất: Nếu mặt phẳng (\alpha) chứa hai đường thẳng cắt nhau a, b và hai đường thẳng này cùng song song với mặt phẳng (\beta) thì mặt phẳng (\alpha) song song với mặt phẳng (\beta).
\left\{ \begin{array}{l}a \subset (\alpha ),b \subset (\alpha )\\a \text{ cắt } b\\a\parallel (\beta ),b\parallel (\beta )\end{array} \right. \Rightarrow (\alpha )\parallel (\beta )
Lời giải chi tiết
Gọi I, J, K lần lượt là trung điểm của BC, CD, BD.
Theo tính chất trọng tâm của tam giác ta có:
\dfrac{AG_1}{AI}=\dfrac{AG_2}{AJ}=\dfrac{AG_3}{AK}=\dfrac{2}{3}.
Theo định lý Ta let suy ra: G_1G_2\parallel IJ mà IJ\subset (BCD)
\Rightarrow G_1G_2\parallel(BCD).
Tương tự ta có G_2G_3\parallel (BCD).
Ta lại có G_1G_2,G_2G_3\subset (G_1G_2G_3)
\Rightarrow (G_1G_2G_3)\parallel (BCD).