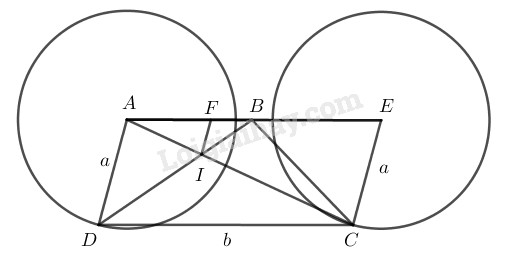
Cho hình thang ABCD có AB song song với CD, AD=a, DC=b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.
LG a
Tìm tập hợp các điểm C khi D thay đổi.
Phương pháp giải:
Sử dụng định nghĩa: T→v(M)=M′⇔→MM′=→v.
Lời giải chi tiết:
Dựng hình bình hành ADCE. Ta có →DC=→AE không đổi.
Do AE=b không đổi, nên E cố định. Do AD=EC=a nên khi D chạy trên đường tròn (A;a) thì C chạy trên đường tròn (E;a) là ảnh của (A;a) qua phép tịnh tiến theo →AE.
LG b
Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a).
Phương pháp giải:
Sử dụng định nghĩa phép vị tự:
Cho I và k≠0. Phép biến hình biến điểm M thành điểm M′ sao cho →IM′=k→IM được gọi là phép vị tự tâm I, tỉ số k.
Lời giải chi tiết:
Đường thẳng qua I , song song với AD cắt AE tại F.
Ta có AIIC=ABCD
⇒AIAI+IC=ABAB+b
⇒AIAC=ABAB+b
⇒→AI=ABAB+b→AC
Do đó có thể xem I là ảnh của C qua phép vị tự tâm A, tỉ số ABAB+b. Vậy khi C chạy trên (E;a) thì I chạy trên đường tròn là ảnh của (E;a) qua phép vị tự nói trên.