Chọn đáp án đúng:
5.105
Cho \(y = \dfrac{{x - 2}}{{x + 3}}\).Tìm y''.
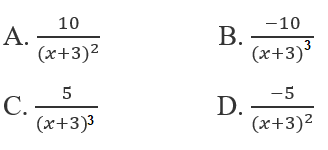
Lời giải chi tiết:
\(\begin{array}{l}y = \dfrac{{x - 2}}{{x + 3}} = \dfrac{{x + 3 - 5}}{{x + 3}}\\ = \dfrac{{x + 3}}{{x + 3}} - \dfrac{5}{{x + 3}} = 1 - \dfrac{5}{{x + 3}}\\y' = - \dfrac{{ - 5\left( {x + 3} \right)'}}{{{{\left( {x + 3} \right)}^2}}} = \dfrac{5}{{{{\left( {x + 3} \right)}^2}}}\\y'' = \dfrac{{ - 5\left( {{{\left( {x + 3} \right)}^2}} \right)'}}{{{{\left( {x + 3} \right)}^4}}}\\ = \dfrac{{ - 5.2\left( {x + 3} \right)\left( {x + 3} \right)'}}{{{{\left( {x + 3} \right)}^4}}}\\ = \dfrac{{ - 10}}{{{{\left( {x + 3} \right)}^3}}}\end{array}\)
Chọn đáp án: B
5.106
Tìm đạo hàm cấp hai của hàm số \(y = \sqrt[3]{x}\)
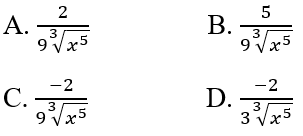
Lời giải chi tiết:
\(\begin{array}{l}y = \sqrt[3]{x} = {x^{\dfrac{1}{3}}}\\y' = \dfrac{1}{3}{x^{\dfrac{1}{3} - 1}} = \dfrac{1}{3}{x^{ - \dfrac{2}{3}}}\\y'' = \dfrac{1}{3}.\left( { - \dfrac{2}{3}} \right){x^{ - \dfrac{2}{3} - 1}}\\ = - \dfrac{2}{9}{x^{ - \dfrac{5}{3}}} = - \dfrac{2}{{9{x^{\dfrac{5}{3}}}}} = - \dfrac{2}{{9\sqrt[3]{{{x^5}}}}}\end{array}\)
Chọn đáp án: C
5.107
Cho hàm số y = sin3x.cosx. Tìm y''.
A. y'' = -8sin4x - 2sin2x
B. y'' = 8sin4x + 2sin2x
C. y'' = -4sin4x - 2sin2x
D. y'' = -8sin4x + 2sin2x
Phương pháp giải:
Biến đổi sin3xcosx = 1/2[sin4x + sin2x].
Lời giải chi tiết:
\(\begin{array}{l}y = \sin 3x\cos x\\ = \dfrac{1}{2}\left( {\sin 4x + \sin 2x} \right)\\y' = \dfrac{1}{2}\left( {4\cos 4x + 2\cos 2x} \right)\\y'' = \dfrac{1}{2}\left[ {4.\left( { - 4\sin 4x} \right) + 2.\left( { - 2\sin 2x} \right)} \right]\\ = - 8\sin 4x - 2\sin 2x\end{array}\)
Chọn đáp án: A
5.108
Tìm đạo hàm cấp hai y'' của \(y = \sqrt x \)

Lời giải chi tiết:
\(\begin{array}{l}y = \sqrt x = {x^{\dfrac{1}{2}}}\\y' = \left( {{x^{\dfrac{1}{2}}}} \right)' = \dfrac{1}{2}{x^{\dfrac{1}{2} - 1}} = \dfrac{1}{2}{x^{ - \dfrac{1}{2}}}\\y'' = \dfrac{1}{2}.\left( { - \dfrac{1}{2}} \right){x^{ - \dfrac{1}{2} - 1}} = - \dfrac{1}{4}{x^{ - \dfrac{3}{2}}}\\ = - \dfrac{1}{{4{x^{\dfrac{3}{2}}}}} = - \dfrac{1}{{4\sqrt {{x^3}} }} = - \dfrac{1}{{4x\sqrt x }}\end{array}\)
Chọn đáp án: D
5.109
Tìm y'', biết \(y = \dfrac{{{x^2}}}{{1 - x}}\)
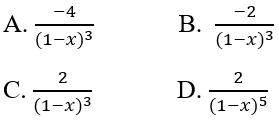
Phương pháp giải:
Có thể chia cho mẫu để được \(y = - x - 1 - \dfrac{1}{{x - 1}}\) trước khi lấy đạo hàm.
Lời giải chi tiết:
\(\begin{array}{l}y = \dfrac{{{x^2}}}{{1 - x}} = \dfrac{{{x^2} - 1 + 1}}{{1 - x}}\\ = \dfrac{{{x^2} - 1}}{{1 - x}} + \dfrac{1}{{1 - x}}\\ = - x - 1 - \dfrac{1}{{x - 1}}\\y' = - 1 - \dfrac{{ - \left( {x - 1} \right)'}}{{{{\left( {x - 1} \right)}^2}}}\\ = - 1 + \dfrac{1}{{{{\left( {x - 1} \right)}^2}}}\\y'' = - \dfrac{{\left[ {{{\left( {x - 1} \right)}^2}} \right]'}}{{{{\left( {x - 1} \right)}^4}}}\\ = - \dfrac{{2\left( {x - 1} \right)\left( {x - 1} \right)'}}{{{{\left( {x - 1} \right)}^4}}}\\ = - \dfrac{2}{{{{\left( {x - 1} \right)}^3}}} = \dfrac{2}{{{{\left( {1 - x} \right)}^3}}}\end{array}\)
Chọn đáp án: C
5.110
Cho hàm số f(x) = cos3x. Tính f''(π/3)
A. -1 B. -2 C. 1/3 D. 9
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = - 3\sin 3x\\f''\left( x \right) = - 3.3\cos 3x\\ = - 9\cos 3x\\f''\left( {\dfrac{\pi }{3}} \right) = - 9\cos \left( {3.\dfrac{\pi }{3}} \right)\\ = - 9\cos \pi = - 9.\left( { - 1} \right) = 9\end{array}\)
Chọn đáp án: D
5.111
Cho hàm số g(t) = sin22t. Tính g''(π/8), g''(π/12)
A. 0; 4 B. 1; 4
C. 1; 2 D. 3; 1
Lời giải chi tiết:
\(\begin{array}{l}g\left( t \right) = {\sin ^2}2t = \dfrac{{1 - \cos 4t}}{2}\\ = \dfrac{1}{2} - \dfrac{1}{2}\cos 4t\\g'\left( t \right) = - \dfrac{1}{2}\left( { - 4\sin 4t} \right) = 2\sin 4t\\g''\left( t \right) = 2.4\cos 4t = 8\cos 4t\\g''\left( {\dfrac{\pi }{8}} \right) = 8\cos \dfrac{\pi }{2} = 0\\g''\left( {\dfrac{\pi }{{12}}} \right) = 8\cos \dfrac{\pi }{3} = 8.\dfrac{1}{2} = 4\end{array}\)
Chọn đáp án: A

