Tính đạo hàm của các hàm số sau:
LG a
\(y = \frac{{1 + x - {x^2}}}{{1 - x + {x^2}}}\)
Lời giải chi tiết:
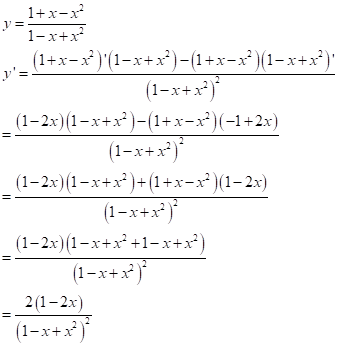
LG b
\(y = \frac{{\left( {2 - {x^2}} \right)\left( {3 - {x^3}} \right)}}{{{{\left( {1 - x} \right)}^2}}}\)
Lời giải chi tiết:
LG c
\(y = \cos 2x - 2\sin x\)
Lời giải chi tiết:
\(\begin{array}{l}y = \cos 2x - 2\sin x\\y' = \left( {\cos 2x} \right)' - 2\left( {\sin x} \right)'\\ = - \left( {2x} \right)'\sin 2x - 2\cos x\\ = - 2\sin 2x - 2\cos x\end{array}\)
LG d
\(y = \frac{{\cos x}}{{2{{\sin }^2}x}}\)
Lời giải chi tiết:
\(\begin{array}{l}y = \frac{{\cos x}}{{2{{\sin }^2}x}}\\y' = \frac{{\left( {\cos x} \right)'.2{{\sin }^2}x - \cos x\left( {2{{\sin }^2}x} \right)'}}{{4{{\sin }^4}x}}\\ = \frac{{ - \sin x.2{{\sin }^2}x - \cos x.2.2\left( {\sin x} \right)'\sin x}}{{4{{\sin }^4}x}}\\ = \frac{{ - 2{{\sin }^3}x - 4\cos x.\cos x.\sin x}}{{4{{\sin }^4}x}}\\ = \frac{{ - 2\sin x\left( {{{\sin }^2}x + 2{{\cos }^2}x} \right)}}{{4{{\sin }^4}x}}\\ = - \frac{{{{\sin }^2}x + {{\cos }^2}x + {{\cos }^2}x}}{{2{{\sin }^3}x}}\\ = - \frac{{1 + {{\cos }^2}x}}{{2{{\sin }^3}x}}\end{array}\)
LG e
\(y = {\cos ^2}\frac{x}{3}\tan \frac{x}{2}\)
Lời giải chi tiết:
\(y = {\cos ^2}\frac{x}{3}\tan \frac{x}{2}\)
\(\begin{array}{l}y' = \left( {{{\cos }^2}\frac{x}{3}} \right)'\tan \frac{x}{2} + {\cos ^2}\frac{x}{3}\left( {\tan \frac{x}{2}} \right)'\\ = 2\cos \frac{x}{3}.\left( {\cos \frac{x}{3}} \right)'.\frac{{\sin \frac{x}{2}}}{{\cos \frac{x}{2}}} + {\cos ^2}\frac{x}{3}.\frac{{\left( {\frac{x}{2}} \right)'}}{{{{\cos }^2}\frac{x}{2}}}\\ = 2\cos \frac{x}{3}.\left( {\frac{x}{3}} \right)'.\left( { - \sin \frac{x}{3}} \right).\frac{{\sin \frac{x}{2}}}{{\cos \frac{x}{2}}} + {\cos ^2}\frac{x}{3}.\frac{{\frac{1}{2}}}{{{{\cos }^2}\frac{x}{2}}}\\ = - 2\cos \frac{x}{3}.\frac{1}{3}\sin \frac{x}{3}.\frac{{\sin \frac{x}{2}}}{{\cos \frac{x}{2}}} + \frac{1}{2}.\frac{{{{\cos }^2}\frac{x}{3}}}{{{{\cos }^2}\frac{x}{2}}}\\ = - \frac{1}{3}\sin \frac{{2x}}{3}\tan \frac{x}{2} + \frac{{{{\cos }^2}\frac{x}{3}}}{{2{{\cos }^2}\frac{x}{2}}}\end{array}\)
LG f
\(y = \sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)}\)
Lời giải chi tiết:
\(\begin{array}{l}y = \sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)} \\y' = \frac{{\left[ {\sin \left( {2x - \frac{\pi }{6}} \right)} \right]'}}{{2\sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)} }}\\ = \frac{{\left( {2x - \frac{\pi }{6}} \right)'.\cos \left( {2x - \frac{\pi }{6}} \right)}}{{2\sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)} }}\\ = \frac{{2\cos \left( {2x - \frac{\pi }{6}} \right)}}{{2\sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)} }}\\ = \frac{{\cos \left( {2x - \frac{\pi }{6}} \right)}}{{\sqrt {\sin \left( {2x - \frac{\pi }{6}} \right)} }}\end{array}\)
LG g
\(y = \cos \frac{x}{{x + 1}}\)
Lời giải chi tiết:
\(y = \cos \frac{x}{{x + 1}}\)
\(\begin{array}{l}y' = \left( {\frac{x}{{x + 1}}} \right)'.\left( { - \sin \frac{x}{{x + 1}}} \right)\\ = \frac{{\left( x \right)'\left( {x + 1} \right) - x\left( {x + 1} \right)'}}{{{{\left( {x + 1} \right)}^2}}}.\left( { - \sin \frac{x}{{x + 1}}} \right)\\ = - \frac{{1.\left( {x + 1} \right) - x.1}}{{{{\left( {x + 1} \right)}^2}}}\sin \frac{x}{{x + 1}}\\ = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\sin \frac{x}{{x + 1}}\end{array}\)
LG h
\(y = \frac{{{x^2} - 1}}{{\sin 3x}}\)
Lời giải chi tiết:
\(y = \frac{{{x^2} - 1}}{{\sin 3x}}\)
\(\begin{array}{l}y' = \frac{{\left( {{x^2} - 1} \right)'\sin 3x - \left( {{x^2} - 1} \right).\left( {\sin 3x} \right)'}}{{{{\sin }^2}3x}}\\ = \frac{{2x\sin 3x - \left( {{x^2} - 1} \right).\left( {3x} \right)'\cos 3x}}{{{{\sin }^2}3x}}\\ = \frac{{2x\sin 3x - \left( {{x^2} - 1} \right).3\cos 3x}}{{{{\sin }^2}3x}}\\ = \frac{{2x\sin 3x - 3\left( {{x^2} - 1} \right)\cos 3x}}{{{{\sin }^2}3x}}\end{array}\)
LG i
\(y = 3{\sin ^2}x\cos x + {\cos ^2}x\)
Lời giải chi tiết:
\(\begin{array}{l}y = 3{\sin ^2}x\cos x + {\cos ^2}x\\y' = 3.\left[ {\left( {{{\sin }^2}x} \right)'\cos x + {{\sin }^2}x\left( {\cos x} \right)'} \right] + 2\cos x\left( {\cos x} \right)'\\ = 3\left[ {2\sin x\left( {\sin x} \right)'\cos x + {{\sin }^2}x.\left( { - \sin x} \right)} \right] + 2\cos x\left( { - \sin x} \right)\\ = 3\left( {2\sin x\cos x\cos x - {{\sin }^3}x} \right) - 2\sin x\cos x\\ = 3\left( {\sin 2x\cos x - {{\sin }^3}x} \right) - \sin 2x\\ = 3\sin 2x\cos x - 3{\sin ^3}x - \sin 2x\\ = \sin 2x\left( {3\cos x - 1} \right) - 3{\sin ^3}x\end{array}\)
LG k
\(y = \sqrt {7 - 4x} \cot 3x\)
Lời giải chi tiết:
\(\begin{array}{l}y = \sqrt {7 - 4x} \cot 3x\\y' = \left( {\sqrt {7 - 4x} } \right)'\cot 3x + \sqrt {7 - 4x} \left( {\cot 3x} \right)'\\ = \frac{{\left( {7 - 4x} \right)'}}{{2\sqrt {7 - 4x} }}.\cot 3x + \sqrt {7 - 4x} .\frac{{ - \left( {3x} \right)'}}{{{{\sin }^2}3x}}\\ = \frac{{ - 4}}{{2\sqrt {7 - 4x} }}.\cot 3x + \sqrt {7 - 4x} .\frac{{ - 3}}{{{{\sin }^2}3x}}\\ = \frac{{ - 2\cot 3x}}{{\sqrt {7 - 4x} }} - \frac{{3\sqrt {7 - 4x} }}{{{{\sin }^2}3x}}\end{array}\)
