Đề bài
Chứng minh rằng tiếp tuyến của hypebol \(y = {{{a^2}} \over x}\) lập thành với các trục toạ độ một tam giác có diện tích không đổi.
Lời giải chi tiết
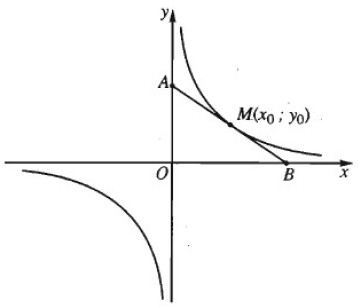
\(\displaystyle y = {{{a^2}} \over x} \Rightarrow y'\left( {{x_0}} \right) = - {{{a^2}} \over {x_0^2}}.\)
Phương trình tiếp tuyến tại \(\displaystyle M\left( {{x_0};{y_0}} \right)\) là
\(\displaystyle \eqalign{
& y - {{{a^2}} \over {{x_0}}} = - {{{a^2}} \over {x_0^2}}\left( {x - {x_0}} \right) \cr
& \Leftrightarrow y = - {{{a^2}x} \over {x_0^2}} + {{2{a^2}} \over {{x_0}}}. \cr} \)
Cho \(\displaystyle x = 0 \Rightarrow y = \dfrac{{2{a^2}}}{{{x_0}}}\) \(\displaystyle \Rightarrow A\left( {0;\dfrac{{2{a^2}}}{{{x_0}}}} \right)\)
Cho \(\displaystyle y = 0 \Rightarrow - \dfrac{{{a^2}x}}{{x_0^2}} + \dfrac{{2{a^2}}}{{{x_0}}} = 0\) \(\displaystyle \Leftrightarrow \dfrac{{{a^2}x}}{{x_0^2}} = \dfrac{{2{a^2}}}{{{x_0}}}\) \(\displaystyle \Leftrightarrow {a^2}x = 2{a^2}{x_0}\) \(\displaystyle \Leftrightarrow x = 2{x_0}\) \(\displaystyle \Rightarrow B\left( {2{x_0};0} \right)\)
Suy ra diện tích tam giác OAB là
\(\displaystyle S = {1 \over 2}.\left| {{{2{a^2}} \over {{x_0}}}} \right|.2\left| {{x_0}} \right| = 2{a^2} = const.\)

