Giải bài 3.22 trang 124 SBT đại số và giải tích 11

147 lượt xem

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Tìm cấp số cộng $\left( {{u_n}} \right)$ biết

LG a

$\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 27\\u_1^2 + u_2^2 + u_3^2 = 275\end{array} \right.$

Phương pháp giải:

Sử dụng tính chất ${u_{k - 1}} + {u_{k + 1}} = 2{u_k}$ .

Lời giải chi tiết:

Đặt $\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 27{\rm{ }}\left( 1 \right)\\u_1^2 + u_2^2 + u_3^2 = 275{\rm{ }}\left( 2 \right)\end{array} \right.$

Ta có:

$\begin{array}{l} {u_1} + {u_2} + {u_3} = 27\\ \Leftrightarrow \left( {{u_1} + {u_3}} \right) + {u_2} = 27\\ \Leftrightarrow 2{u_2} + {u_2} = 27\\ \Leftrightarrow 3{u_2} = 27\\ \Leftrightarrow {u_2} = 9 \end{array}$

Thay ${u_2} = 9$ vào (1) và (2) ta được $\left\{ \begin{array}{l}{u_1} + {u_3} = 18\,\,(3)\\u_1^2 + u_3^2 = 194\,\,(4)\end{array} \right.$

$\left( 3 \right) \Rightarrow {u_3} = 18 - {u_1}$ thay vào (4) ta được:

$\begin{array}{l}u_1^2 + {\left( {18 - {u_1}} \right)^2} = 194\\ \Leftrightarrow u_1^2 + 324 - 36{u_1} + u_1^2 = 194\\ \Leftrightarrow 2u_1^2 - 36{u_2} + 130 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{u_1} = 5\\{u_1} = 13\end{array} \right.\end{array}$

Với ${u_1} = 5 \Rightarrow {u_3} = 13$ ta có CSC $5;9;13$

Với ${u_1} = 13 \Rightarrow {u_3} = 5$ ta có CSC $13;9;5$ .

Vậy ta có hai cấp số cộng $5,9,13$ và $13,9,5.$

LG b

$\left\{ \begin{array}{l}{u_1} + {u_2} + ... + {u_n} = a\\u_1^2 + u_2^2 + ... + u_n^2 = {b^2}\end{array} \right.$ .

Phương pháp giải:

Sử dụng công thức ${u_n} = {u_1} + \left( {n - 1} \right)d$ .

Lời giải chi tiết:

Ta có:

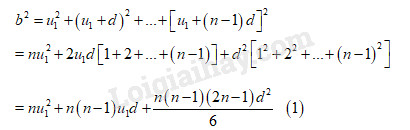
Mặt khác, $a = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}$ $\Rightarrow 2a = 2n{u_1} + \left( {n - 1} \right)d$ $\Leftrightarrow {u_1} = \dfrac{{2a - \left( {n - 1} \right)d}}{{2n}}$ .

Thay ${u_1}$ vào (1) ta được:

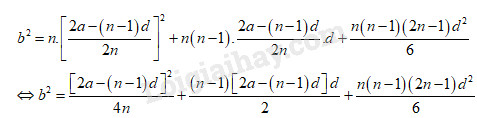
Kết quả $d = \pm \sqrt {\dfrac{{12\left( {n{b^2} - {a^2}} \right)}}{{{n^2}\left( {{n^2} - 1} \right)}}}$ ; ${u_1} = \dfrac{1}{n}\left[ {a - \dfrac{{n\left( {n - 1} \right)}}{2}d} \right]$

SBT Toán lớp 11