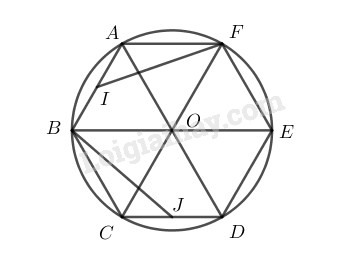
Cho lục giác đều \(ABCDEF\), \(O\) là tâm đối xứng của nó, \(I\) là trung điểm của \(AB\)
LG a
Tìm ảnh của tam giác \(AIF\) qua phép quay tâm \(O\) góc \({120}^o\)
Phương pháp giải:
Sử dụng định nghĩa:
Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết:
Phép quay tâm \(O\) góc \({120}^o\) biến \(F\), \(A\), \(B\) lần lượt thành \(B\), \(C\), \(D\); biến trung điểm \(I\) của \(AB\) thành trung điểm \(J\) của \(CD\). Nên nó biến tam giác \(AIF\) thành tam giác \(CJB\).
LG b
Tìm ảnh của tam giác \(AOF\) qua phép quay tâm \(E\) góc \({60}^o\)
Phương pháp giải:
Sử dụng định nghĩa:
Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết:
Phép quay tâm \(E\) góc \({60}^o\) biến \(A\), \(O\), \(F\) lần lượt thành \(C\), \(D\), \(O\).