Đề bài
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
\(\displaystyle {{AM} \over {AC}} = {{BN} \over {B{\rm{D}}}} = k\left( {k > 0} \right)\)
Chứng minh rằng ba vectơ \(\displaystyle \overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
Phương pháp giải - Xem chi tiết
Chứng minh \(\displaystyle \overrightarrow {PQ} = m\overrightarrow {PM} +n\overrightarrow {PN} \) và sử dụng điều kiện đồng phẳng của ba véc tơ và kết luận.
Lời giải chi tiết
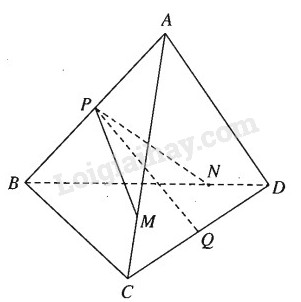
Ta có:
\(\displaystyle \eqalign{
& \overrightarrow {PQ} = {1 \over 2}\left( {\overrightarrow {PC} + \overrightarrow {P{\rm{D}}} } \right) \cr
& = {1 \over 2}\left[ {\left( {\overrightarrow {AC} - \overrightarrow {AP} } \right) + \left( {\overrightarrow {B{\rm{D}}} - \overrightarrow {BP} } \right)} \right] \cr
& = {1 \over 2}\left[ {\left( {\overrightarrow {AC} + \overrightarrow {B{\rm{D}}} } \right) - \underbrace {\left( {\overrightarrow {AP} + \overrightarrow {BP} } \right)}_{\overrightarrow 0 }} \right] \cr
& = {1 \over 2}.{1 \over k}\left( {\overrightarrow {AM} + \overrightarrow {BN} } \right) \cr} \)
Vì \(\displaystyle \overrightarrow {AC} = {1 \over k}.\overrightarrow {AM} \) và \(\displaystyle \overrightarrow {B{\rm{D}}} = {1 \over k}.\overrightarrow {BN} \)
Đồng thời \(\displaystyle \overrightarrow {AM} = \overrightarrow {AP} + \overrightarrow {PM} \) và \(\displaystyle \overrightarrow {BN} = \overrightarrow {BP} + \overrightarrow {PN} \), nên \(\displaystyle \overrightarrow {PQ} = {1 \over {2k}}\left( {\overrightarrow {PM} + \overrightarrow {PN} } \right)\) vì \(\displaystyle \overrightarrow {AP} + \overrightarrow {BP} = \overrightarrow 0 \)
Vậy \(\displaystyle \overrightarrow {PQ} = {1 \over {2k}}\overrightarrow {PM} + {1 \over {2k}}\overrightarrow {PN} \)
Do đó ba vectơ \(\displaystyle \overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
