Đề bài
Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng \(AC = BC = A{\rm{D}} = B{\rm{D}} = a\) và \(AB = p,C{\rm{D}} = q\).
Lời giải chi tiết
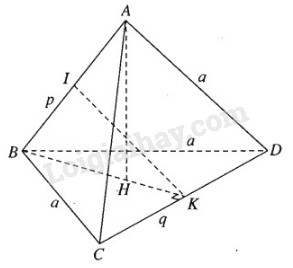
Gọi I và K lần lượt là trung điểm của AB và CD.
Ta có: \(\Delta ACD = \Delta BCD\left( {c - c - c} \right)\) nên \(AK = BK\) (hai đường trung tuyến tương ứng)
\( \Rightarrow \Delta ABK\) cân tại \(K\) có \(I\) là trung điểm \(AB\) nên \(KI \bot AB\).
Tương tự ta có \(IK \bot CD\) nên \(IK\) là đoạn vuông góc chung của \(AB,CD\).
Độ dài đoạn IK là khoảng cách cần tìm:
\(I{K^2} = B{K^2} - B{I^2} = B{K^2} - {{{p^2}} \over 4}\)
Mà \(B{K^2} = B{C^2} - C{K^2} = {a^2} - {{{q^2}} \over 4}\)
Vậy \(I{K^2} = {a^2} - {{{p^2} + {q^2}} \over 4}\)
Do đó \(IK = {1 \over 2}\sqrt {4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right)} \)
Với điều kiện \(4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right) > 0\).

