Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD\), đáy lớn là \(AD\) và \(AD = 2BC\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(G\) là trọng tâm của tam giác \(SCD\).
LG a
Chứng minh rằng \(OG\parallel \left( {SBC} \right)\).
Phương pháp giải:
Sử dụng định lý Talet.
Sử dụng tính chất của trọng tâm.
Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).
Lời giải chi tiết:
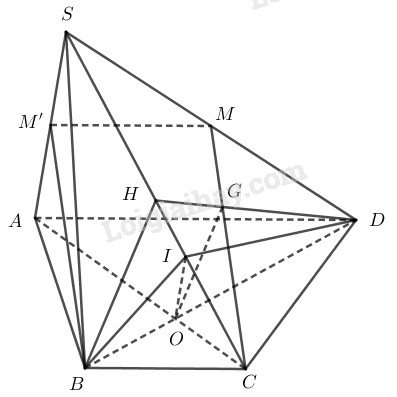
Tứ giác \(ABCD\) là hình thang có \(AD\parallel =2BC\).
Theo định lý Talet \(\dfrac{OD}{OB}=\dfrac{OA}{OC}=\dfrac{AD}{BC}=2\)
\(\Rightarrow \dfrac{OD}{BD}=\dfrac{OD}{OB+OD}\) \(=\dfrac{2}{1+2}=\dfrac{2}{3}\text{(1)}\).
Gọi \(H\) là trung điểm của \(SC\), tam giác \(SCD\) có \(G\) là trọng tâm nên \(\dfrac{DG}{DH}=\dfrac{2}{3}\text{(2)}\).
Từ \(\text{(1)}\) và \(\text{(2)}\) suy ra \(\dfrac{DO}{DB}=\dfrac{DG}{DH}=\dfrac{2}{3}\)
Theo định lý Talet \(OG\parallel BH\text{(*)}\).
Mà \(H\in SC\Rightarrow H\in (SBC)\)
\(\Rightarrow BH\subset (SBC)\text{(**)}\)
Từ \(\text{(*)}\) và \(\text{(**)}\) suy ra \( OG\parallel (SBC)\).
LG b
Cho \(M\) là trung điểm của \(SD\). Chứng minh rằng \(CM\parallel \left( {SAB} \right)\).
Phương pháp giải:
Sử dụng tính chất đường trung bình trong tam giác.
Sử dụng tính chất hình bình hành.
Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).
Lời giải chi tiết:
Gọi \(M’\) là trung điểm của \(SA\) và ta có \(M\) là trung điểm \(SD\) nên trong tam giác \(SAD\) khi đó \(MM’\) là đường trung bình.
\(\Rightarrow MM’\parallel =\dfrac{1}{2}AD\)
Mà hình thang \(ABCD\) có \(BC\parallel =\dfrac{1}{2}AD\)
Suy ra \(MM’\parallel =BC\) \(\Rightarrow\) tứ giác \(MM’BC\) là hình bình hành.
\(\Rightarrow MC\parallel M’B\)
Ta lại có \(M’B\subset (SAB)\)
\(\Rightarrow MC\parallel (SAB)\).
LG c
Giả sử điểm \(I\) nằm trong đoạn \(SC\) sao cho \(S{\rm{C = }}\dfrac{3 }{2}SI\). Chứng minh rằng \(SA\parallel \left( {BI{\rm{D}}} \right)\).
Phương pháp giải:
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).
Lời giải chi tiết:
Ta có: \(SC=\dfrac{3}{2}SI\) \(\Rightarrow \dfrac{CI}{CS}=\dfrac{1}{3}\).
Mà \(\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{2}\) nên \(\dfrac{CO}{CA}=\dfrac{1}{3}\).
Suy ra \(\dfrac{CI}{CS}=\dfrac{CO}{CA}=\dfrac{1}{3}\)
Theo định lý Talet ta được \(IO\parallel SA\) mà \(IO\subset (BID)\)
\(\Rightarrow SA\parallel (BID)\).

