Đề bài
Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I,J,K thẳng hàng.
Phương pháp giải - Xem chi tiết
Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt.
Lời giải chi tiết
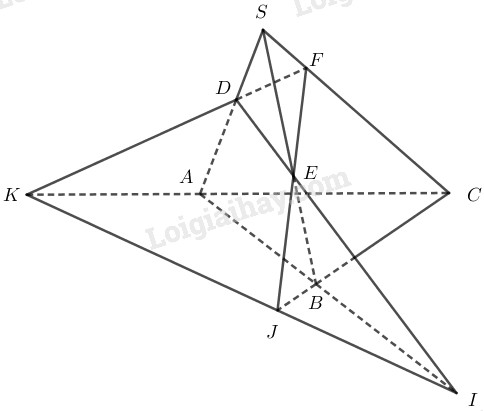
Ta có: I=DE∩AB
Mà DE⊂(DEF)⇒I∈(DEF)
và AB⊂(ABC)⇒I∈(ABC)
Suy ra I∈(DEF)∩(ABC)
Ta có: J=EF∩BC
Mà EF⊂(DEF)⇒J∈(DEF)
và BC⊂(ABC)⇒J∈(ABC)
Suy ra J∈(DEF)∩(ABC)
Tương tự, K∈(DEF)∩(ABC) nên I, J, K thuộc giao tuyến của (ABC) và (DEF) nên I, J, K thẳng hàng.

