Đề bài
Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho IAID=JBJC. Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định.
Phương pháp giải - Xem chi tiết
Sử dụng định lý talet.
Sử dụng tính chất: Nếu đường thẳng d không năm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song với (α).
\left\{ \begin{array}{l}d \not\subset (\alpha )\\d\parallel d'\\d' \subset (\alpha )\end{array} \right. \Rightarrow d\parallel (\alpha )
Sử dụng tính chất khi (\alpha) song song với (\beta) thì (\alpha) sẽ song song với mọi đường thẳng nằm trong (\beta).
Lời giải chi tiết
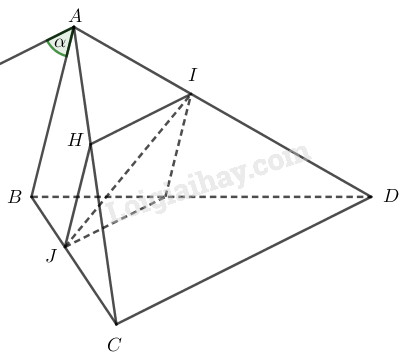
Qua I kẻ đường thẳng song song với CD cắt AC tại H nên ta có:
\dfrac{HA}{HC}=\dfrac{IA}{ID}.
Mà \dfrac{IA}{ID}=\dfrac{JB}{JC}.
Từ đó suy ra \dfrac{HA}{HC}=\dfrac{JB}{JC}.
Theo định lý Talet suy ra HJ\parallel AB mà HJ\subset (IJH) \Rightarrow AB\parallel (IJH) \text{ (1)}
Theo cách dựng IH\parallel CD, IH\subset (IJH) \Rightarrow CD\parallel (IJH) \text{ (2)}
Từ \text{(1)} và \text{(2)} suy ra (IJH)\parallel AB, CD.
Gọi (\alpha) là mặt phẳng đi qua AB và song song với CD.
Ta có:
\left\{ \begin{array}{l}(\alpha )\parallel ({\rm{IJ}}H)\\{\rm{IJ}} \subset ({\rm{IJ}}H)\end{array} \right. \Rightarrow {\rm{IJ}}\parallel (\alpha )
Vậy IJ song song với mặt phẳng (\alpha) cố định.
