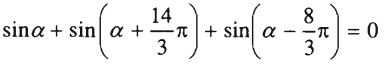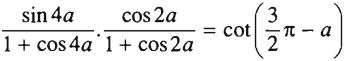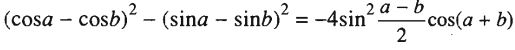Chứng minh các hệ thức sau:
LG a
Lời giải chi tiết:
\(\begin{array}{l}
\sin \alpha + \sin \left( {\alpha + \frac{{14\pi }}{3}} \right) + \sin \left( {\alpha - \frac{{8\pi }}{3}} \right)\\
= \sin \alpha + \sin \left( {\alpha + \frac{{2\pi }}{3} + 4\pi } \right) + \sin \left( {\alpha - \frac{{2\pi }}{3} - 2\pi } \right)\\
= \sin \alpha + \sin \left( {\alpha + \frac{{2\pi }}{3}} \right) + \sin \left( {\alpha - \frac{{2\pi }}{3}} \right)\\
= \sin \alpha + 2\sin \alpha \cos \frac{{2\pi }}{3}\\
= \sin \alpha + 2\sin \alpha .\left( { - \frac{1}{2}} \right)\\
= \sin \alpha - \sin \alpha = 0
\end{array}\)
LG b
Lời giải chi tiết:
\(\begin{array}{l}
VT = \frac{{\sin 4\alpha }}{{1 + \cos 4\alpha }}.\frac{{\cos 2\alpha }}{{1 + \cos 2\alpha }}\\
= \frac{{2\sin 2\alpha \cos 2\alpha }}{{2{{\cos }^2}2\alpha }}.\frac{{\cos 2\alpha }}{{2{{\cos }^2}\alpha }}\\
= \frac{{\sin 2\alpha }}{{2{{\cos }^2}\alpha }} = \frac{{2\sin \alpha \cos \alpha }}{{2{{\cos }^2}\alpha }}\\
= \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha \\
VP = \cot \left( {\frac{{3\pi }}{2} - \alpha } \right)\\
= \cot \left( {\pi + \frac{\pi }{2} - \alpha } \right)\\
= \cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \\
\Rightarrow VT = VP\left( {dpcm} \right)
\end{array}\)
LG c
Lời giải chi tiết:
\(\begin{array}{l}
VT = {\left( {\cos a - \cos b} \right)^2} - {\left( {\sin a - \sin b} \right)^2}\\
= {\left( { - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}} \right)^2} - {\left( {2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}} \right)^2}\\
= 4{\sin ^2}\frac{{a + b}}{2}{\sin ^2}\frac{{a - b}}{2} - 4{\cos ^2}\frac{{a + b}}{2}{\sin ^2}\frac{{a - b}}{2}\\
= 4{\sin ^2}\frac{{a - b}}{2}\left( {{{\sin }^2}\frac{{a + b}}{2} - {{\cos }^2}\frac{{a + b}}{2}} \right)\\
= - 4{\sin ^2}\frac{{a - b}}{2}\left( {{{\cos }^2}\frac{{a + b}}{2} - {{\sin }^2}\frac{{a + b}}{2}} \right)\\
= - 4{\sin ^2}\frac{{a - b}}{2}.\cos \left( {a + b} \right)=VP
\end{array}\)
LG d
Lời giải chi tiết:
\(\begin{array}{l}
VT = {\sin ^2}\left( {{{45}^0} + \alpha } \right) - {\sin ^2}\left( {{{30}^0} - \alpha } \right)\\
- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= \left[ {\sin \left( {{{45}^0} + \alpha } \right) - \sin \left( {{{30}^0} - \alpha } \right)} \right].\\
.\left[ {\sin \left( {{{45}^0} + \alpha } \right) + \sin \left( {{{30}^0} - \alpha } \right)} \right]\\- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= 2\cos \frac{{{{75}^0}}}{2}\sin \frac{{{{15}^0} + 2\alpha }}{2}.2\sin \frac{{{{75}^0}}}{2}\cos \frac{{{{15}^0} + 2\alpha }}{2}\\
- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= \left( {2\sin \frac{{{{75}^0}}}{2}\cos \frac{{{{75}^0}}}{2}} \right).\left( {2\sin \frac{{{{15}^0} + 2\alpha }}{2}\cos \frac{{{{15}^0} + 2\alpha }}{2}} \right)\\
- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= \sin {75^0}.\sin \left( {{{15}^0} + 2\alpha } \right)- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= \cos {15^0}.\sin \left( {{{15}^0} + 2\alpha } \right)- \sin {15^0}.\cos \left( {{{15}^0} + 2\alpha } \right)\\
= \sin \left( {{{15}^0} + 2\alpha - {{15}^0}} \right) = \sin 2\alpha =VP
\end{array}\)