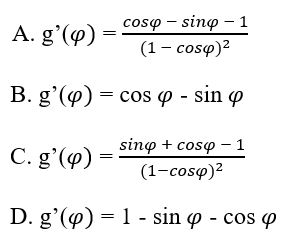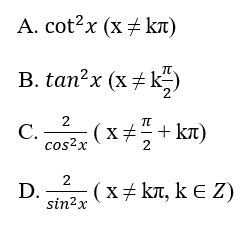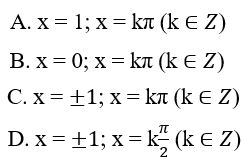Chọn đáp án đúng:
5.70
Tìm đạo hàm của hàm số y=sinx2x
Lời giải chi tiết:
y′=(sinx2)′.x−sinx2.(x)′x2=(x2)′cosx2.x−sinx2x2=2xcosx2.x−sinx2x2=2x2cosx2−sinx2x2
Chọn đáp án: A
5.71
Cho hàm số y=cosxx+1. Tìm y'
Lời giải chi tiết:
y′=(xx+1)′(−sinxx+1)=(x)′(x+1)−x(x+1)′(x+1)2(−sinxx+1)=x+1−x(x+1)2(−sinxx+1)=−sinxx+1(x+1)2
Chọn đáp án: C
5.72
Tìm đạo hàm của hàm số y = tan2 x – cot x2
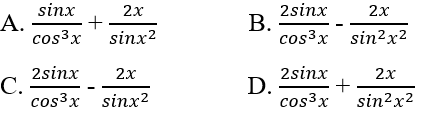
Lời giải chi tiết:
y′=2tanx(tanx)′−(x2)′.(−1sin2x2)=2tanx.1cos2x+2xsin2x2=2.sinxcosx.1cos2x+2xsin2x2=2sinxcos3x+2xsin2x2
Chọn đáp án: D
5.73
Cho f(t)=cost1−sint. Tính f'(π/6)
A. -2 B. -3 C. 2 D. 5
Lời giải chi tiết:
f′(t)=(cost)′(1−sint)−cost.(1−sint)′(1−sint)2=−sint(1−sint)−cost(−cost)(1−sint)2=−sint+sin2t+cos2t(1−sint)2=−sint+1(1−sint)2=11−sint⇒f′(π6)=11−sinπ6=11−12=2
Chọn đáp án: C
5.74
Tìm đạo hàm của hàm số y = (3 - sinx)3
A. 3(3 - sinx)
B. -3(3 - sinx)2cosx
C. -3(3 - sinx).cosx
D. -3(3 - sinx).cos2x
Lời giải chi tiết:
y′=3(3−sinx)2(3−sinx)′=3(3−sinx)2(0−cosx)=−3(3−sinx)2cosx
Chọn đáp án: B
5.75
Cho f(x)=√1+2tanx. Tính f'(π/4)

Lời giải chi tiết:
f′(x)=(1+2tanx)′2√1+2tanx=2.(tanx)′2√1+2tanx=1cos2x√1+2tanx=1cos2x√1+2tanx⇒f′(π4)=1cos2π4√1+2tanπ4=1(√22)2.√1+2.1=2√3=2√33
Chọn đáp án: D
5.76
Tìm đạo hàm của g(φ)=cosφ+sinφ1−cosφ
Lời giải chi tiết:
g′(φ)=(cosφ+sinφ)′(1−cosφ)−(cosφ+sinφ)(1−cosφ)′(1−cosφ)2=(−sinφ+cosφ)(1−cosφ)−(cosφ+sinφ)(−(−sinφ))(1−cosφ)2=−sinφ+cosφ+sinφcosφ−cos2φ−cosφsinφ−sin2φ(1−cosφ)2=−sinφ+cosφ−(cos2φ+sin2φ)(1−cosφ)2=cosφ−sinφ−1(1−cosφ)2
Chọn đáp án: A
5.77
Cho y=cot√1+x2. Tính y'(1)
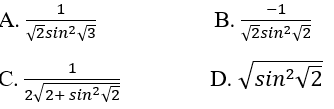
Lời giải chi tiết:
y′=(√1+x2)′.(−1sin2√1+x2)=(1+x2)′2√1+x2.(−1sin2√1+x2)=2x2√1+x2.(−1sin2√1+x2)=−x√1+x2.sin2√1+x2⇒y′(1)=−1√2sin2√2
Chọn đáp án: B
5.78
Cho f(x) = 5x2 - 16√x + 7. Tính f'(4); f'(1/4)
A. 36; -27/2
B. -36; 27/2
C. 1; 35
D. 36; -2
Lời giải chi tiết:
f′(x)=5.2x−16.12√x=10x−8√x⇒f′(4)=10.4−8√4=36f′(14)=10.14−8√14=−272
Chọn đáp án: A
5.79
Cho g(x) = x2sin(x - 2). Tính g'(2).
A. -2 B. 4 C. 2 D. 1
Lời giải chi tiết:
g′(x)=(x2)′sin(x−2)+x2[sin(x−2)]′=2xsin(x−2)+x2.cos(x−2)⇒g′(2)=2.2sin0+22cos0=0+4.1=4
Chọn đáp án: B
5.80
Tìm đạo hàm của hàm số y=tanx2−cotx2
Lời giải chi tiết:
y′=(x2)′.1cos2x2−(x2)′.(−1sin2x2)=12.1cos2x2+12.1sin2x2=12(1cos2x2+1sin2x2)=12.sin2x2+cos2x2cos2x2.sin2x2=24cos2x2.sin2x2=2(2cosx2sinx2)2=2sin2x
Chọn đáp án: D
5.81
Giải phương trình f'(x) = g(x), biết
g(x) = sinx và f(x) = (2 - x2)cosx + 2x.sinx.
Lời giải chi tiết:
f′(x)=(2−x2)′cosx+(2−x2)(cosx)′+2((x)′sinx+x(sinx)′)=−2xcosx+(2−x2)(−sinx)+2(sinx+xcosx)=−2xcosx−2sinx+x2sinx+2sinx+2xcosx=x2sinx⇒f′(x)=x2sinxf′(x)=g(x)⇔x2sinx=sinx⇔x2sinx−sinx=0⇔(x2−1)sinx=0⇔[x2−1=0sinx=0⇔[x=±1x=kπ,k∈Z
Chọn đáp án: C