Đề bài
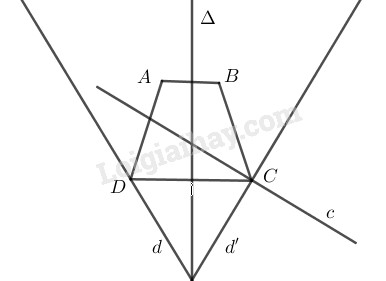
Cho hai đường thẳng \(c\), \(d\) cắt nhau và hai điểm \(A\), \(B\) không thuộc hai đường thẳng đó. Hãy dựng điểm \(C\) trên \(c\), điểm \(D\) trên \(d\) sao cho tứ giác \(ABCD\) là hình thang cân nhận \(AB\) là một cạnh đáy (không cần biện luận).
Phương pháp giải - Xem chi tiết
Để dựng một điểm \(M\) ta tìm cách xác định nó như là ảnh của một điểm đã biết qua một phép đối xứng trục, hoặc xem điểm \(M\) như là giao của một đường cố định với ảnh của một đường đã biết qua một phép đối xứng trục.
Lời giải chi tiết
Ta thấy rằng \(B\), \(C\) theo thứ tự là ảnh của \(A\), \(D\) qua phép đối xứng qua đường trung trực của cạnh \(AB\), từ đó suy ra cách dựng:
- Dựng đường trung trực \(\Delta\) của đoạn \(AB\)
- Dựng \(d’\) là ảnh của \(d\) qua phép đối xứng qua trục \(\Delta\).
Gọi \(C=d’\cap c\).
- Dựng \(D\) là ảnh của \(C\) qua phép đối xứng qua trục \(\Delta\).