Đề bài
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt \(\left( \alpha \right)\) ở A và cắt \(\left( \beta \right)\) ở B ta lấy hai diểm cố định S1,S2 không thuộc \(\left( \alpha \right)\), \(\left( \beta \right)\). Gọi M là một điểm di động trên \(\left( \beta \right)\). Giả sử các đường thẳng \(M{S_1},M{S_2}\) cắt \(\left( \alpha \right)\) lần lượt tại M1 và M2.
a) Chứng minh rằng M1M2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng \(\left( \beta \right)\) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M1 và M2 di động trên hai đường thẳng cố định thuộc mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(M_1M_2\) đi qua \(A\) cố định.
b) Chứng minh \(K\) thuộc giao tuyến của \((M,d)\) và \((\beta )\).
Lời giải chi tiết
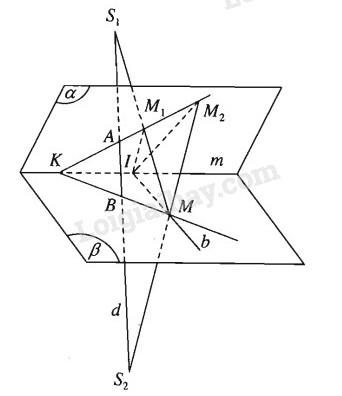
a) Mặt phẳng (M, d) cắt \(\left( \alpha \right)\) theo giao tuyến M1M2. Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M1M2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt \(\left( \beta \right)\) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng (S1, b) luôn luôn cắt \(\left( \alpha \right)\) theo giao tuyến IM1. Do đó điểm M1 di động trên giao tuyến của IM1 cố định. Còn khi M di động trên b thì mặt phẳng (S2, b) cắt \(\left( \alpha \right)\) theo giao tuyến IM2. Do đó điểm M2 chạy trên giao tuyến IM2 cố định.

