Đề bài
Cho tứ diện \(ABCD\) và điểm \(M\) nằm trong tam giác \(BCD\).
a) Dựng đường thẳng qua \(M\) song song với hai mặt phẳng \((ABC)\) và \((ABD)\). Giả sử đường thẳng này cắt mặt phẳng \((ACD)\) tại \(B’\).
Chứng minh rằng \(AB’\), \(BM\) và \(CD\) đồng quy tại một điểm.
b) Chứng minh \(\dfrac{MB'}{BA}= \dfrac{dt\left( {\Delta MC{\rm{D}}} \right)}{dt\left( {\Delta BC{\rm{D}}} \right)}\).
c) Đường thẳng song song với hai mặt phẳng \((ACB)\) và \((ACD)\) kẻ từ \(M\) cắt \((ABD)\) tại \(C’\) và đường thẳng song song với hai mặt phẳng \((ADC)\) và \(ADB)\) kẻ từ \(M\) cắt \((ABC)\) tại \(D’\).
Chứng minh rằng \(\dfrac{MB'}{BA} + \dfrac{MC'}{CA} + \dfrac{M{\rm{D}}'}{DA} = 1\) .
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
\(\left\{ \begin{array}{l} (\alpha )\parallel d\\(\beta )\parallel d\\(\alpha ) \cap (\beta )=d'\end{array} \right. \Rightarrow d\parallel d'\)
Sử dụng định lý Talet.
Lời giải chi tiết
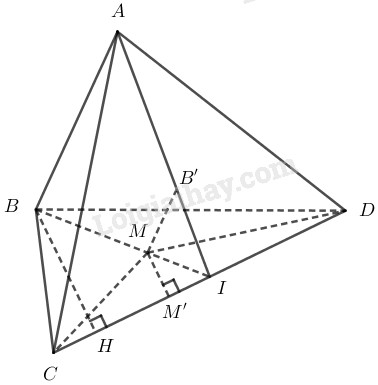
a) Ta có:
\(\left\{ \begin{array}{l}MB'\parallel (ABC )\\MB'\parallel (ABD)\\(ABC) \cap (ABD)=AB\end{array} \right. \)
\(\Rightarrow MB'\parallel AB\)
Do \(MB'\parallel AB\) nên \(MB’\) và \(AB\) xác định một mặt phẳng. Gọi \(MB\cup AB’\equiv I\).
Khi đó \(I \in BM \Rightarrow I \in \left( {BCD} \right)\)
\(I \in AB' \Rightarrow I \in \left( {ACD} \right)\)
Nên \(I \in \left( {BCD} \right) \cap \left( {ACD} \right) = CD\),
\(I \in CD\)
Vậy ba đường thẳng \(AB’\), \(BM\) và \(CD\) đồng quy tại \(I\).
b) \(MB'\parallel AB \Rightarrow \dfrac{MB'}{AB} = \dfrac{IM} {IB}\)
Kẻ \(MM' \bot CD\) và \(BH \bot CD\)
Ta có: \(MM'\parallel BH \Rightarrow \dfrac{IM}{IB} = \dfrac{MM'}{BH}\)
Mặt khác:
\(\left\{ \begin{array}{l}dt(\Delta MCD)=\dfrac{1}{2}CD.MM'\\dt(\Delta BCD)=\dfrac{1}{2}CD.BH\end{array} \right.\)
\(\Rightarrow\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}=\dfrac{\dfrac{1}{2}CD.MM'}{\dfrac{1}{2}CD.BH}\)
\(=\dfrac{MM'}{BH}\)
Do đó: \(\dfrac{MB'} {AB} = \dfrac{IM}{IB} \)
\(= \dfrac{MM'}{BH}= \dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}\).
Vậy \(\dfrac{MB'}{AB} =\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}\).
c) Tương tự ta có:
\(\dfrac{MC'}{CA} =\dfrac {dt(\Delta MBD)}{dt(\Delta BCD)}\)
\(\dfrac{MD'}{DA} =\dfrac {dt(\Delta MBC)}{dt(\Delta BCD)}\)
Vậy:
\(\dfrac{MB'}{BA} + \dfrac{MC'}{CA} + \dfrac{M{\rm{D}}'}{DA}\)
\(=\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}+\dfrac {dt(\Delta MBD)}{dt(\Delta BCD)}+\dfrac {dt(\Delta MBC)}{dt(\Delta BCD)}\)
\(=\dfrac{dt(\Delta MCD)+dt(\Delta MBD)+dt(\Delta MBC)}{dt(\Delta BCD)}\)
\(=1\) .
Logiaihay.com

