Đề bài
Cho tứ diện \(ABCD\) có \(I\) và \(J\) lần lượt là trọng tâm các tam giác \(ABC\) và \(ABD\). Chứng minh rằng: \(IJ \parallel CD\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của trong tâm.
Sử dụng định lý Talet.
Lời giải chi tiết
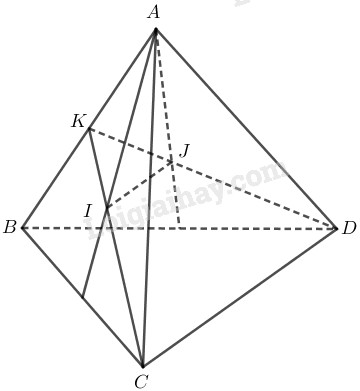
Gọi \(K\) là trung điểm của \(AB\).
Vì \(I\) là trọng tâm của tam giác \(ABC\) nên \(I \in KC\) và vì \(J\) là trọng tâm của tam giác \(ABD\) nên \(J \in KD\).
Từ đó suy ra trong tam giác \(CKD\) ta có
\(\dfrac{{KI}}{{KC}} = \dfrac{{KJ}}{{KD}} = \dfrac{1}{3} \Rightarrow {\rm{IJ}}\parallel CD\).

