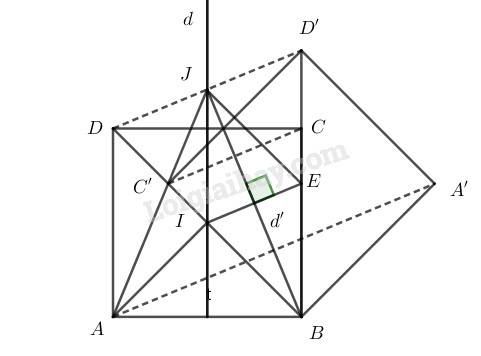
Cho hình vuông \(ABCD\) có tâm \(I\). Trên tia \(BC\) lấy điểm \(E\) sao cho \(BE=AI\)
LG a
Xác định một phép dời hình biến \(A\) thành \(B\) và \(I\) thành \(E\).
Phương pháp giải:
- Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết:
Gọi \(F\) là phép đối xứng qua đường trung trực \(d\) của cạnh \(AB\), \(G\) là phép đối xứng qua đường trung trực \(d’\) của cạnh \(IE\). Khi đó \(F\) biến \(AI\) thành \(BI\), \(G\) biến \(BI\) thành \(BE\). Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình \(F\) và \(G\) sẽ biến \(AI\) thành \(BE\).
Hơn nữa gọi \(J\) là giao của \(d\) và \(d’\), ta có \(JA=JB\), \(JI=JE\) và \(2(JI,JB)=(JI,JE)={45}^o\)
(vì \(JE \parallel IB\)). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm \(J\) góc \({45}^o\).
LG b
Dựng ảnh của hình vuông \(ABCD\) qua phép dời hình ấy.
Phương pháp giải:
- Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết:
Phép biến hình \(F\) biến các điểm \(A\), \(B\), \(C\), \(D\) thành \(B\), \(A\), \(D\), \(C\); \(G\) biến các điểm \(B\), \(A\), \(D\), \(C\) thành \(B\), \(A’\), \(D’\), \(C’\). Do đó ảnh của hình vuông \(ABCD\) qua phép dời hình nói trên là hình vuông \(BA’D’C’\) đối xứng với hình vuông \(BADC\) qua \(d'\).