Đề bài
Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \(M\) và \(N\) lần lượt là trung điểm của hai cạnh bên \(AA’\) và \(CC’\). Một điểm \(P\) nằm trên cạnh bên \(DD’\).
a) Xác định giao điểm \(Q\) của đường thẳng \(BB’\) với mặt phẳng \((MNP)\).
b) Mặt phẳng \((MNP)\) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng \((MNP)\) với mặt phẳng \((ABCD)\) của hình hộp.
Phương pháp giải - Xem chi tiết
Tìm giao điểm của đường thẳng \(d\) và mặt phẳng \((\alpha)\) ta tìm giao điểm của hai đường thẳng \(d\) và \(d'\) trong đó \(d'\subset (\alpha)\).
Sử dụng tính chất: Cho hai mặt phẳng song song với nhau. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết
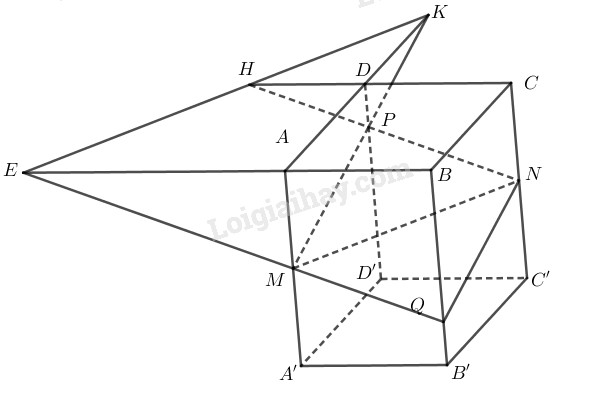
a) Ta có \((AA’, DD’)\parallel (BB’, CC’)\)
\((MNP)\cap (AA’, DD’)=MP\)
Suy ra giao tuyến của \((MNP)\) và \((BB’, CC’)\) song song với \(MP\).
Ta có \(N\in (MNP)\cap (BB',CC')\)
\(\Rightarrow (MNP)\cap (BB',CC')=Nx\),
\(Nx\parallel MP\).
\(\Rightarrow (MNP)\cap (BB',CC')\)
\(=Nx\cap BB'=Q\)
b) Ta có
\((MNP)\cap AA'\), \(BB'\), \(CC'\), \(DD'\) lần lượt tại \(M\), \(P\), \(N\), \(Q\).
\(\Rightarrow (MNP)\) cắt hình hộp theo thiết diện \(MPNQ\).
Ta có
\(\left\{ \begin{array}{l} (AA’, BB’)\parallel (DD’, CC’)\\(MNP)\cap (AA’, BB’)=MQ\\(MNP)\cap (DD’, CC’)=PN\end{array} \right.\)
\(\Rightarrow MQ\parallel PN\)
Mà theo câu a) \(MP\parallel NQ\)
\(\Rightarrow\) tứ giác \(MQNP\) là hình bình hành.
Vậy \((MNP)\) cắt hình hộp theo thiết diện \(MPNQ\) là hình bình hành.
c) Th1: \(P\) không phải là trung điểm của \(DD'\)
Gọi \(H = PN \cap DC,K = MP \cap AD\). Ta có \(d = HK\) là giao tuyến của mặt phẳng (MNP) với mặt phẳng \((ABCD)\) của hình hộp. Chú ý rằng giao điểm \(E = AB \cap MQ\) cũng nằm trên giao tuyến \(d\) nói trên.
Th2: \(P\) là trung điểm của \(DD'\)
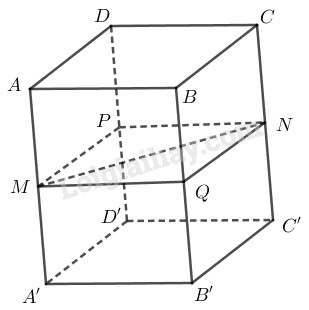
Khi đó \(MP\parallel AD, AD\subset (ABCD)\)
\(\Rightarrow MP\parallel (ABCD)\)
Và \(PN\parallel DC, DC\subset (ABCD)\)
\(\Rightarrow PN\parallel (ABCD)\)
Mà \(MP, PN\subset (MNP)\)
\(\Rightarrow (MNP)\parallel (ABCD)\) khi đó hai mặt phẳng không có giao tuyến.

