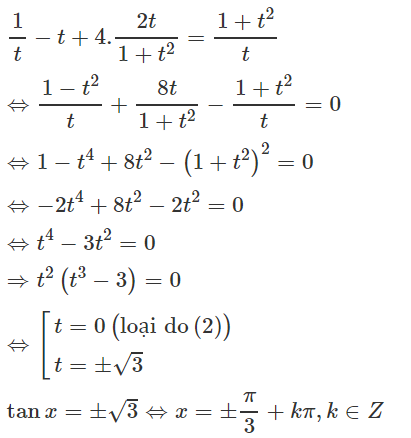Đề bài
Giải phương trình \(\cot x-\tan x+4\sin 2x=\dfrac{2}{\sin 2x}\)
Phương pháp giải - Xem chi tiết
Tìm ĐKXĐ của phương trình.
Sử dụng công thức \(\tan x=\dfrac{\sin x}{\cos x}\) và \(\cot x=\dfrac{\cos x}{\sin x}\) để biến đổi phương trình.
Sử dụng công thức nhân đôi.
Sử dụng công thức \({\sin}^2 x+{\cos}^2 x=1\).
Lời giải chi tiết
ĐKXĐ: \(\sin x\ne 0\) và \(\cos x\ne 0\) \(\Leftrightarrow \sin 2x\ne 0\)
\(\Leftrightarrow \cos 2x\ne \pm 1\)
Ta có: \(\cot x-\tan x+4\sin 2x=\dfrac{2}{\sin 2x}\)
\(\Leftrightarrow \dfrac{\cos x}{\sin x}-\dfrac{\sin x}{\cos x}+4\sin 2x=\dfrac{2}{\sin 2x} \)
\(\Leftrightarrow \dfrac{{\cos}^2 x-{\sin}^2 x}{\sin x\cos x}+4\sin 2x=\dfrac{2}{\sin 2x} \)
\(\Leftrightarrow \dfrac{\cos 2x}{\dfrac{\sin 2x}{2}}+4\sin 2x=\dfrac{2}{\sin 2x} \)
\(\Leftrightarrow \dfrac{2\cos 2x}{\sin 2x}+4\sin 2x=\dfrac{2}{\sin 2x} \)
\(\Leftrightarrow 2\cos 2x+4{\sin}^2 2x=2\)
\(\Leftrightarrow 2\cos 2x+4(1-{\cos}^2 2x)=2\)
\(\Leftrightarrow 4{\cos}^2 2x-2\cos 2x+2=0\)
\(\Leftrightarrow \left[ \begin{array}{l} \cos 2x=1\text{(loại)}\\\cos 2x=-\dfrac{1}{2}\end{array} \right. \)
\(\Leftrightarrow 2x=\pm\dfrac{2\pi}{3}+k2\pi,k\in\mathbb{Z}\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k\pi,k\in\mathbb{Z}\).
Cách khác:
Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng