Đề bài
Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.
Phương pháp giải - Xem chi tiết
Chứng minh hai chiều:
- Giả sử \(M\) cách đều \(A,B,C\) suy ra \(M\) nằm trên đường thẳng vuông góc với \((ABC)\) tại tâm đường tròn ngoại tiếp tam giác \(ABC\).
- Giả sử \(M\) thuộc đường thẳng vuông góc với \((ABC)\) tại tâm đường tròn ngoại tiếp tam giác \(ABC\) và chứng minh \(M\) cách đều \(A,B,C\).
Lời giải chi tiết
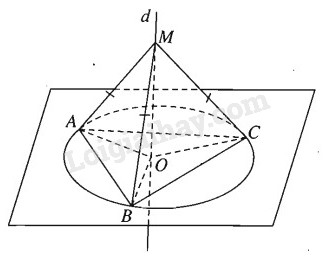
Phần thuận. Nếu MA = MB = MC nghĩa là M cách đều ba đỉnh của tam giác ABC và MO vuông góc với mặt phẳng (ABC) thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Từ đó ta suy ra OA = OB = OC nghĩa là A, B, C nằm trên đường tròn tâm O ngoại tiếp tam giác ABC.
Vậy điểm M cách đều ba đỉnh của tam giác ABC thì nằm trên đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn ngoại tiếp tam giác ABC.
Phần đảo. Nếu ta lấy một điểm M bất kì thuộc đường thẳng d nói trên thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Do đó ta suy ra MA = MB = MC nghĩa là điểm M cách đều ba đỉnh của tam giác ABC.
Kết luận. Tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó. Người ta thường gọi đường thẳng d là trục của đường tròn (C).

