Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD=3AM.
LG a
Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
Phương pháp giải:
Sử dụng tính chất: Nếu hai mặt phẳng lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết:
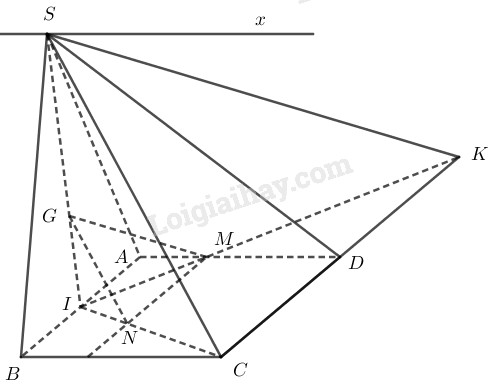
Ta có S=(SAD)∩(SBC)
{AD⊂(SAD)BC⊂(SBC)AD∥BC
⇒(SAD)∩(SBC)=Sx;
Sx∥AD∥BC.
LG b
Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng NG∥(SCD).
Phương pháp giải:
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song (α).
Lời giải chi tiết:
Ta có: MN∥AI∥CD theo định lý Talet ta được INIC=AMAD=13.
Mặt khác: G là trọng tâm tam giác SAB nên IGIS=13.
Suy ra: INIC=IGIS=13.
Theo định lý Talet ta được GN∥SC mà SC⊂(SCD).
⇒GN∥(SCD).
LG c
Chứng minh rằng MG∥(SCD)
Phương pháp giải:
Sử dụng định lý Talet.
Sử dụng tính chất: Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song (α).
Lời giải chi tiết:
Gọi K=IM∩CD ⇒K∈CD ⇒K∈(SCD) ⇒SK⊂(SCD)
Ta có MN∥CD
Theo Talet ta có MNCK=INIC=13
⇒IMIK=13
Mà G là trong tâm tam giác SAB nên IGIS=13
Suy ra IMIK=IGIS=13
⇒GM∥SK mà SK⊂(SCD).
Nên GM∥(SCD).

