Đề bài
Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc α,0≤α<2π, biến hình chữ nhật trên thành chính nó?
A. Không có B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
Phương pháp giải - Xem chi tiết
Vẽ hình và nhận xét.
Lời giải chi tiết
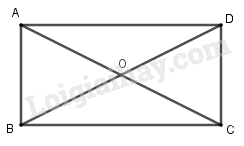
Ta thấy, Q(O,0)(A)=A, Q(O,0)(B)=B, Q(O,0)(C)=C, Q(O,0)(D)=D
Nên Q(O,0)(ABCD)=ABCD.
Q(O,π)(A)=C, Q(O,π)(B)=D, Q(O,π)(C)=A, Q(O,π)(D)=B
Nên Q(O,0)(ABCD)=CDAB.
Vậy có 2 phép quay cần tìm.
Chọn B.

