Đề bài
Cho hình chóp S.ABCD có đáy là hình thang (đáy lớn AD). Gọi O là giao điểm của AC và BD, I và J lần lượt là trung điểm của SB và SC.
a) Xác định giao điểm M của AI và (SCD).
b) Chứng minh IJ∥(SAD).
c) Xác định thiết diện của hình chóp cắt bởi mp (P) qua I, song song với SD và AC.
Phương pháp giải - Xem chi tiết
a) Mở rộng mặt phẳng (SCD), từ đó tìm giao điểm M.
b) Chứng minh IJ song song với một đường thẳng nằm trong (SAD).
c) Xác định giao tuyến của (P) với các mặt của hình chóp.
Lời giải chi tiết
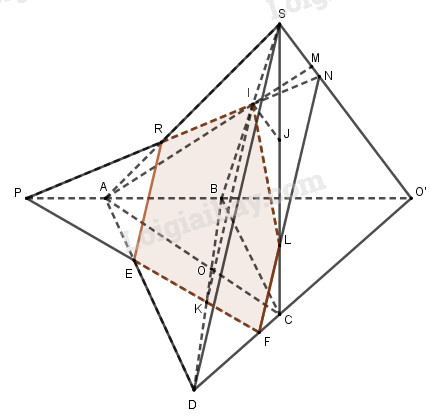
a) Gọi O′=AB∩CD.
Ta có:
{O′∈AB⊂(SAB)O′∈CD⊂(SCD) ⇒O′∈(SAB)∩(SCD)
Mà S∈(SAB)∩(SCD) nên SO′=(SAB)∩(SCD)
Trong (SAB) gọi M=AI∩SO′
⇒{M∈AIM∈SO′⊂(SCD) ⇒M=AI∩(SCD)
b) Tam giác SBC có I, J lần lượt là trung điểm SB, SC nên IJ là đường trung bình của tam giác SBC.
Do đó IJ//BC. Mà BC//AD nên IJ//AD
Mà AD⊂(SAD) nên IJ//(SAD).
c)
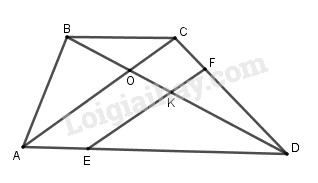
Đường thẳng qua I song song với SD cắt BD tại K.
Do OBOD=BCAD<1 nên OB<OD.
Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA,DC,BA lần lượt tại E,F,P.
Gọi R=IP∩SA. Kéo dài PI cắt SO′ tại N
Gọi L=NF∩SC
Ta có thiết diện là ngũ giác IREFL.

