Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA′=a, trên By lấy đoạn BB′=b, trên Cz lấy đoạn CC′=c.
LG a
Gọi I, J và K lần lượt là các giao điểm B′C′, C′A′ và A′B′ với (α).
Chứng minh rằng IBIC.JCJA.KAKB=1
Phương pháp giải:
Sử dụng tính chất của hai tam giác đồng dạng.
Lời giải chi tiết:
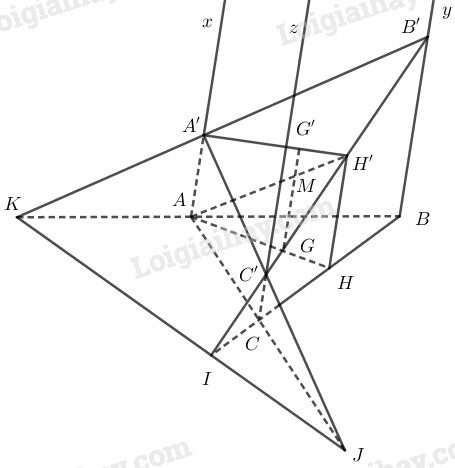
Ta có:
CC′∥BB′⇒ΔICC′∼ΔIBB′
⇒IBIC=BB′CC′=bc
CC′∥AA′⇒ΔJCC′∼ΔJAA′
⇒JCJA=CC′AA′=ca
AA′∥BB′⇒ΔKAA′∼ΔKBB′
⇒KAKB=AA′BB′=ab
Do đó: IBIC.JCJA.KAKB=bc.ca.ab=1
LG b
Gọi G và G′ lần lượt là trọng tâm của các tam giác ABC và A′B′C′.
Chứng minh: GG′∥AA′.
Phương pháp giải:
Sử dụng tính chất đường trung bình của tam giác.
Sử dụng tính chất của trong tâm trong tam giác.
Sử dụng định lý Talet.
Lời giải chi tiết:
Gọi H và H′ lần lượt là trung điểm của các cạnh BC và B′C′. Vì HH′ là đường trung bình của hình thang BB′CC′ nên HH′∥BB′.
Mà BB′∥AA′ suy ra HH′∥AA′
Ta có: G∈AH và G′∈A′H′ và ta có:
{AGAH=23A′G′A′H′=23⇒AA′∥GG′∥HH′
LG c
Tính GG′ theo a, b, c.
Phương pháp giải:
Chia đoạn GG′ thành hai đoạn thuộc hai tam giác.
Sử dụng định lý Talet để tính từng cạnh đó.
Lời giải chi tiết:
AH′∩GG′=M
⇒GG′=G′M+MG
Ta có: G′M∥AA′⇒ΔH′G′M∼ΔH′A′A
⇒G′MAA′=H′G′H′A′=13
⇒G′M=13AA′=13a
MG∥HH′⇒ΔAMG∼ΔAH′H
⇒MGHH′=AGAH=23
⇒MG=23HH′
Mặt khác HH′ là đường trung bình của hình thang BB′CC′ nên
HH′=BB′+CC′2=b+c2
⇒MG=23HH′
=23.b+c2
=13(b+c)
Do đó: GG′=G′M+MG
=13a+13(b+c)
=13(a+b+c)
Vậy GG′=13(a+b+c).

