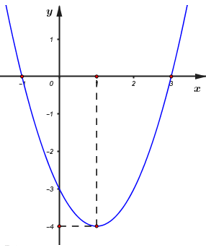
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu giá trị \(m\) nguyên để phương trình \(\left| {f\left( x \right) + 1} \right| = m\) có 4 nghiệm phân biệt?
Phương trình \(\left| {f\left( x \right) + 1} \right| = m\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( P \right):y = \left| {f\left( x \right) + 1} \right|\) và đường thẳng \(d:y = m\) cắt nhau tại 4 điểm phân biệt
\(\left( P \right):y = \left| {f\left( x \right) + 1} \right|\) có được bằng cách
Bước 1: Dịch đồ thị lên trên 1 đơn vị
Bước 2: Giữ nguyên phần nằm trên đồ thị; lấy đối xứng phần nằm dưới đồ thị qua Ox
Bước 3: Gạch bỏ phần nằm dưới trục \(Ox\)
Dựa vào đồ thị hàm số ta thấy: đường thẳng \(d:\,\,y = m\) cắt đồ thị hàm số \(y = \left| {f\left( x \right) + 1} \right|\) tại \(4\) điểm phân biệt \( \Leftrightarrow 0 < m < 3\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2} \right\} \Rightarrow \) có 2 giá trị \(m\) thỏa mãn bài toán.
Một giá đỡ được gắn vào bức tường như hình vẽ. Tam giác \(ABC\) vuông cân ở đỉnh \(C\). Người ta treo vào điểm \(A\) một vật có trọng lượng \(10\;{\rm{N}}\). Khi đó lực tác động vào bức tường tại hai điểm \(B\) và \(C\) có cường độ lần lượt là:


Tại điểm \(A\) có lực kéo \(\overrightarrow F \) hướng thẳng đứng xuống dưới với cường độ \(10N\)
Ta có \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) với hai véc tơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) là các véc tơ lần lượt cùng phương với hai đường thẳng \(AC,AB\)
Vì \(ABC\) vuông cân tại \(C\) nên \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right| = 10N\) và \(\left| {\overrightarrow {{F_2}} } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow F } \right|}^2}} = 10\sqrt 2 \)
Vậy cường độ lực tại \(C\) bằng cường độ lực tại \(A\) và bằng \(10\;{\rm{N}}\).
Cường độ lực tại \(B\) bằng \(10\sqrt 2 \;{\rm{N}}\).
Tìm \(m\) để hàm số \(y = {x^2} - 2x + 2m + 3\) có giá trị nhỏ nhất trên đoạn \(\left[ {2\,;\,5} \right]\) bằng \( - 3\).
Ta có bảng biến thiên của hàm số \(y = {x^2} - 2x + 2m + 3\) trên đoạn \(\left[ {2\,;\,5} \right]\):

Do đó giá trị nhỏ nhất trên đoạn \(\left[ {2\,;\,5} \right]\) của hàm số \(y = {x^2} - 2x + 2m + 3\) bằng \(2m + 3\).
Theo giả thiết \(2m + 3 = - 3\)\( \Leftrightarrow m = - 3\).
Xác định các hệ số \(a\) và \(b\) để Parabol \(\left( P \right):y = a{x^2} + 4x - b\) có đỉnh \(I\left( { - 1; - 5} \right)\).
Ta có: \({x_I} = - 1 \Rightarrow - \dfrac{4}{{2a}} = - 1 \Rightarrow a = 2.\)
Hơn nữa: \(I \in \left( P \right)\) nên \( - 5 = a - 4 - b \Rightarrow b = 3.\)
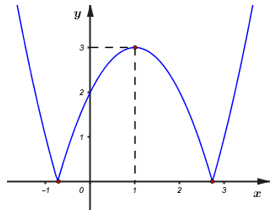
Cho parabol $\left( P \right):y = a{x^2} + bx + c$$\left( {a \ne 0} \right)$ có đồ thị như hình bên. Tìm các giá trị $m$ để phương trình $\left| {a{x^2} + bx + c} \right| = m$ có bốn nghiệm phân biệt.

Quan sát đồ thị ta có đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) là là phần đồ thị phía trên trục hoành của $\left( P \right)$ và phần có được do lấy đối xứng phần phía dưới trục hoành của $\left( P \right)$, như hình vẽ sau:

Phương trình $\left| {a{x^2} + bx + c} \right| = m$ có bốn nghiệm phân biệt khi đường thẳng $y = m$ cắt đồ thị hàm số hàm số $y = \left| {a{x^2} + bx + c} \right|$ tại bốn điểm phân biệt.
Suy ra \(0 < m < 3\).
Tìm tất cả các giá trị \(m\) để đường thẳng \(y = mx + 3 - 2m\) cắt parabol \(y = {x^2} - 3x - 5\) tại \(2\) điểm phân biệt có hoành độ trái dấu.
Phương trình hoành độ giao điểm: \({x^2} - 3x - 5 = mx + 3 - 2m\) \( \Leftrightarrow \) \({x^2} - \left( {m + 3} \right)x + 2m - 8 = 0\,\,\,\left( * \right)\).
Đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ trái dấu khi và chỉ khi phương trình \(\left( * \right)\) có hai nghiệm trái dấu \( \Leftrightarrow \) \(a.c < 0\) \( \Leftrightarrow \) \(2m - 8 < 0\) \( \Leftrightarrow \) \(m < 4\).
Đường thẳng \(d:y = \left( {m - 3} \right)x - 2m + 1\) cắt hai trục tọa độ tại hai điểm \(A\) và \(B\) sao cho tam giác \(OAB\) cân. Khi đó, số giá trị của \(m\) thỏa mãn là
\(A = d \cap Ox\) nên tọa độ \(A\) là nghiệm của hệ:
\(\left\{ \begin{array}{l}y = \left( {m - 3} \right)x - 2m + 1\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{2m - 1}}{{m - 3}}\\y = 0\end{array} \right.\) nên \(A\left( {\dfrac{{2m - 1}}{{m - 3}};{\rm{ }}0} \right)\).
\(B = d \cap Oy\) nên tọa độ \(B\) là nghiệm của hệ:
\(\left\{ \begin{array}{l}y = \left( {m - 3} \right)x - 2m + 1\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = - 2m + 1\end{array} \right.\) nên \(B\left( {0; - 2m + 1} \right)\).
Ta có \(OA = OB\)\( \Leftrightarrow \left| {\dfrac{{2m - 1}}{{m - 3}}} \right| = \left| { - 2m + 1} \right| \Leftrightarrow \left| {2m - 1} \right|\left( {\dfrac{1}{{\left| {m - 3} \right|}} - 1 = 0} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}2m - 1 = 0\\\left| {m - 3} \right| = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{2}\\m = 4,{\rm{ }}m = 2\end{array} \right.\).
Nhận xét: Với \(m = \dfrac{1}{2}\)thì \(A \equiv B \equiv O\left( {0;\;0} \right)\) nên không thỏa mãn.
Vậy \(m = 4,{\rm{ }}m = 2\).
Các đường thẳng \(y = - 5\left( {x + 1} \right)\); \(y = 3x + a\); \(y = ax + 3\) đồng quy với giá trị của \(a\) là
Gọi \({d_1}:y = - 5x - 5\), \({d_2}:y = 3x + a\), ${d_3}:y = ax + 3$ \(\left( {a \ne 3} \right)\).
Phương trình hoành độ giao điểm của \({d_1}\) và \({d_2}\): \( - 5x - 5 = 3x + a\)\( \Leftrightarrow x = \dfrac{{ - a - 5}}{8}\).
Giao điểm của \({d_1}\) và \({d_2}\) là \(A\left( {\dfrac{{ - a - 5}}{8};\dfrac{{5a - 15}}{8}} \right)\).
Đường thẳng \({d_1}\), \({d_2}\) và \({d_3}\) đồng qui khi \(A \in {d_3}\) \( \Leftrightarrow \dfrac{{5a - 15}}{8} = a.\dfrac{{ - a - 5}}{8} + 3\)\( \Leftrightarrow {a^2} + 10a - 39 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}a = 3\\a = - 13\end{array} \right.\) \( \Leftrightarrow a = - 13\). (vì \(a \ne 3\))
Tìm $m$ để hàm số \(y = \dfrac{{\sqrt {x - 2m + 3} }}{{x - m}} + \dfrac{{3x - 1}}{{\sqrt { - x + m + 5} }}\) xác định trên khoảng \(\left( {0;1} \right)\).
Gọi \(D\) là tập xác định của hàm số \(y = \dfrac{{\sqrt {x - 2m + 3} }}{{x - m}} + \dfrac{{3x - 1}}{{\sqrt { - x + m + 5} }}\).
ĐKXĐ: \(\left\{ \begin{array}{l}x - 2m + 3 \ge 0\\x - m\not = 0\\ - x + m + 5 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2m - 3\\x\not = m\\x < m + 5\end{array} \right.\).
*Hàm số \(y = \dfrac{{\sqrt {x - 2m + 3} }}{{x - m}} + \dfrac{{3x - 1}}{{\sqrt { - x + m + 5} }}\) xác định trên khoảng \(\left( {0;1} \right)\)
\( \Leftrightarrow \)\(\left( {0;1} \right) \subset D\)$ \Leftrightarrow \left\{ \begin{array}{l}2m - 3 \le 0\\m + 5 \ge 1\\m \notin \left( {0;1} \right)\end{array} \right.$\( \Leftrightarrow \left\{ \begin{array}{l}m \le \dfrac{3}{2}\\m \ge - 4\\\left[ \begin{array}{l}m \ge 1\\m \le 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow m \in \left[ { - 4;0} \right] \cup \left[ {1;\dfrac{3}{2}} \right]\).
Tìm các giá trị thực của tham số $m$ để hàm số $y = \dfrac{{x + m + 2}}{{x - m}}$ xác định trên $\left( { - 1;\,2} \right)$.
Hàm số $y = \dfrac{{x + m + 2}}{{x - m}}$ xác định khi $x \ne m$ hay TXĐ \(D = \left( { - \infty ;m} \right) \cup \left( {m; + \infty } \right)\)
Hàm số $y = \dfrac{{x + m + 2}}{{x - m}}$ xác định trên $\left( { - 1;\,2} \right)$ khi và chỉ khi $\left( { - 1;2} \right) \subset D$$ \Leftrightarrow \left( { - 1;2} \right) \subset \left( { - \infty ;m} \right) \cup \left( {m; + \infty } \right) \Leftrightarrow \left[ \begin{array}{l}\left( { - 1;2} \right) \subset \left( { - \infty ;m} \right)\\\left( { - 1;2} \right) \subset \left( {m; + \infty } \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge 2\\m \le - 1\end{array} \right.$
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là \(27\) (triệu đồng) và bán ra với giá là \(31\) triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là \(600\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm \(200\) chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
Gọi \(x\) (triệu) đồng là số tiền mà doanh nghiệp A dự định giảm giá; \(\left( {0 \le x \le 4} \right)\).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là \(31 - x - 27\)\( = 4 - x\) (triệu đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là \(600 + 200x\) (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là
\(f\left( x \right) = \left( {4 - x} \right)\left( {600 + 200x} \right)\)\( = - 200{x^2} + 200x + 2400\).
Xét hàm số \(f\left( x \right) = - 200{x^2} + 200x + 2400\) trên đoạn \(\left[ {0;4} \right]\) có bảng biến thiên

Vậy \(\mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = 2\,450\)\( \Leftrightarrow x = \dfrac{1}{2}\).
Vậy giá mới của chiếc xe là \(30,5\) triệu đồng thì lợi nhuận thu được là cao nhất.
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng \(162\,{\rm{m}}\). Trên thành cổng, tại vị trí có độ cao \(43\,{\rm{m}}\) so với mặt đất (điểm \(M\)), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn \(10\,{\rm{m}}\). Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).
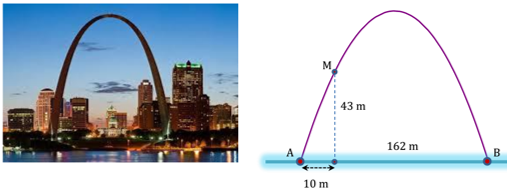
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
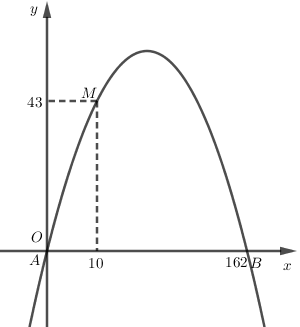
Phương trình Parabol \(\left( P \right)\) có dạng \(y = a{x^2} + bx + c\).
Parabol \(\left( P \right)\) đi qua điểm \(A\left( {0;0} \right)\), \(B\left( {162;0} \right)\), \(M\left( {10;43} \right)\) nên ta có
\(\left\{ \begin{array}{l}c = 0\\{162^2}a + 162b + c = 0\\{10^2}a + 10b + c = 43\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \dfrac{{43}}{{1520}}\\b = \dfrac{{3483}}{{760}}\end{array} \right.\)\( \Rightarrow \left( P \right):y = - \dfrac{{43}}{{1520}}{x^2} + \dfrac{{3483}}{{760}}x\).
Do đó chiều cao của cổng là \(h = - \dfrac{\Delta }{{4a}}\)\( = - \dfrac{{{b^2} - 4ac}}{{4a}}\)\( \approx 185,6m.\)
Đồ thị hàm số $y = x - 2m + 1$ tạo với hệ trục tọa độ $Oxy$ tam giác có diện tích bằng $\dfrac{{25}}{2}$. Khi đó $m$ bằng
Gọi: $A$, $B$ lần lượt là giao điểm của đồ thị hàm số $y = x - 2m + 1$ với trục hoành và trục tung
Suy ra $A\left( {2m - 1;\,0} \right)$; $B\left( {0;\,1 - 2m} \right)$.
Theo giả thiết thì tam giác có diện tích bằng $\dfrac{{25}}{2}$ là tam giác $OAB$ vuông tại $O$.
Do đó: ${S_{OAB}} = \dfrac{1}{2}.OA.OB = \dfrac{{25}}{2}$
$ \Leftrightarrow OA.OB = 25$$ \Leftrightarrow \left| {2m - 1} \right|.\left| {1 - 2m} \right| = 25$$ \Leftrightarrow \left| {2m - 1} \right|.\left| {2m - 1} \right| = 25$
$ \Leftrightarrow {\left( {2m - 1} \right)^2} = 25$$ \Leftrightarrow \left[ \begin{array}{l}2m - 1 = 5\\2m - 1 = - 5\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = - 2\end{array} \right.$.
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ $Oth$, trong đó \(t\) là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; \(h\) là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2{\rm{m}}\). Sau đó \(1\) giây, nó đạt độ cao \(8,5{\rm{m}}\) và $2$ giây sau khi đá lên, nó ở độ cao \(6{\rm{m}}\). Hãy tìm hàm số bậc hai biểu thị độ cao \(h\) theo thời gian \(t\) và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
Tại \(t = 0\) ta có \(h = 1,2\); tại \(t = 1\) ta có \(h = 8,5\); tại \(t = 2\), ta có \(h = 6\).
Parabol \(\left( P \right)\) có phương trình: \(h= a{t^2} + bt + c\), với \(a \ne 0\).
Giả sử tại thời điểm \(t'\) thì quả bóng đạt độ cao lớn nhất \(h'\).
Theo bài ra ta có: tại \(t = 0\) thì \(h = 1,2\) nên \(A\left( {0;\,\,1,2} \right) \in \left( P \right)\).
Tại \(t = 1\) thì \(h = 8,5\) nên \(B\left( {1;\,\,8,5} \right) \in \left( P \right)\).
Tại \(t = 2\) thì \(h = 6\) nên \(C\left( {2;\,\,6} \right) \in \left( P \right)\).
Vậy ta có hệ: $\left\{ {\begin{array}{*{20}{c}}{c = 1,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{a + b + c = 8,5}\\{4a + 2b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 1,2\,\,\,\,\,\,\,}\\{a = - 4,9\,}\\{b = 12,2\,}\end{array}} \right.$.
Vậy hàm số cần tìm có dạng: $h = - 4,9{t^2} + 12,2t + 1,2$ hay $y = - 4,9{t^2} + 12,2t + 1,2$
Hỏi có bao nhiêu giá trị $m$ nguyên trong nửa khoảng $\left( {0;2017} \right]$ để phương trình $\left| {{x^2} - 4} \right|x\left| { - 5} \right| - m = 0$ có hai nghiệm phân biệt?
PT: $\left| {{x^2} - 4} \right|x\left| { - 5} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 4} \right|x\left| { - 5} \right| = m\left( 1 \right)$
Số nghiệm phương trình \(\left( 1 \right) \) bằng số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\) và đường thẳng \(y = m\) (cùng phương \(Ox\)).
Xét hàm số \(y = {x^2} - 4x - 5\,\,\left( {{P_1}} \right)\) có đồ thị như hình 1.

Xét hàm số \(y = {x^2} - 4\left| x \right| - 5\,\,\left( {{P_2}} \right)\) là hàm số chẵn nên có đồ thị nhận \(Oy\) làm trục đối xứng. Mà \(y = {x^2} - 4\left| x \right| - 5 = {x^2} - 4x - 5\) nếu \(x \ge 0\). Suy ra đồ thị hàm số \(\left( {{P_2}} \right)\) gồm hai phần:
+) Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_1}} \right)\) phần bên phải \(Oy\).
+) Phần \(2\): Lấy đối xứng phần \(1\) qua trục \(Oy\).
Ta được đồ thị \(\left( {{P_2}} \right)\) như hình 2.
Xét hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\), ta có: \(y = \left\{ \begin{array}{l}{x^2} - 4\left| x \right| - 5\,\,\,\,\,\,\,\,\,\,\left( {y \ge 0} \right)\\ - \left( {{x^2} - 4\left| x \right| - 5} \right)\,\,\left( {y < 0} \right)\end{array} \right.\).
Suy ra đồ thị hàm số \(\left( P \right)\) gồm hai phần:
+) Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_2}} \right)\) phần trên \(Ox\).
+) Phần \(2\): Lấy đối xứng đồ thị hàm số \(\left( {{P_2}} \right)\) phần dưới \(Ox\) qua trục \(Ox\).
Ta được đồ thị \(\left( P \right)\) như hình 3.
Quan sát đồ thị hàm số \(\left( P \right)\) ta có:
Để $\left| {{x^2} - 4} \right|x\left| { - 5} \right| = m\,\,\,\left( 1 \right)$ có hai nghiệm phân biệt\( \Leftrightarrow \left[ \begin{array}{l}m > 9\\m = 0\end{array} \right.\).
Mà \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left( {0;\,2017} \right]\end{array} \right. \) \(\Rightarrow m \in \left\{ {10;\,11;\,12;\,...;\,2017} \right\}\).
Vậy có $2008$ giá trị của $m$ thỏa mãn.
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\). Điểm \(P\left( {\dfrac{a}{b};0} \right)\) (với \(\dfrac{a}{b}\) là phân số tối giản, $b>0$) trên trục hoành thỏa mãn tổng khoảng cách từ \(P\) tới hai điểm \(A\) và \(B\) là nhỏ nhất. Tính \(S = a + b\).
Ta có \(A\), \(B\) nằm cùng phía so với \(Ox\).
Điểm \(A'\left( {1;\,\, - 2} \right)\) đối xứng với điểm \(A\) qua \(Ox\).
Ta có: \(PA + PB = PA' + PB\)
Do đó, để \(PA + PB\) nhỏ nhất thì: 3 điểm \(P,A',B\) thẳng hàng.
\( \Rightarrow \overrightarrow {PA'} \), \(\overrightarrow {PB} \) cùng phương.
$\overrightarrow {PA'} = \left( {\dfrac{{b - a}}{b};\,\, - 2} \right),\,\,\,\overrightarrow {PB} = \left( {\dfrac{{3b - a}}{b};\,\,4} \right)$
\( \Rightarrow \dfrac{{b - a}}{{3b - a}} = - \dfrac{1}{2} \Rightarrow 2b - 2a = - 3b + a \Rightarrow \dfrac{a}{b} = \dfrac{5}{3} \Rightarrow a = 5,b = 3\)
Cho hàm số \(y = {x^2} - 2\left( {m + \dfrac{1}{m}} \right)x + m\)\(\left( {m > 0} \right)\) xác định trên \(\left[ { - 1;1} \right]\). Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên \(\left[ { - 1;1} \right]\) lần lượt là \({y_1}\), \({y_2}\) thỏa mãn \({y_1} - {y_2} = 8\). Khi đó giá trị của \(m\) bằng
Đặt \(y = f\left( x \right) = {x^2} - 2\left( {m + \dfrac{1}{m}} \right)x + m\).
Hoành độ đỉnh của đồ thị hàm số là \(x = m + \dfrac{1}{m}\)\( \ge 2\) (bất đẳng thức Côsi).
Vì hệ số \(a = 1\)\( > 0\) nên hàm số nghịch biến trên \(\left( { - \infty ;m + \dfrac{1}{m}} \right)\).
Suy ra, hàm số nghịch biến \(\left[ { - 1;1} \right]\).
\( \Rightarrow {y_1} = f\left( { - 1} \right)\)\( = 3m + \dfrac{2}{m} + 1\).
\({y_2} = f\left( 1 \right)\)\( = 1 - m - \dfrac{2}{m}\).
Theo đề bài ta có: \({y_1} - {y_2} = 8\) \( \Leftrightarrow \)\(3m + \dfrac{2}{m} + 1 - 1 + m + \dfrac{2}{m} = 8\)\(\left( {m > 0} \right)\)\( \Leftrightarrow {m^2} - 2m + 1 = 0\)\( \Leftrightarrow m = 1\).