Bài tập cuối chương IV

Vì $E$ thuộc đoạn $BC$ và \(BE = 2EC\) suy ra \(\overrightarrow {BE}  = 2\overrightarrow {EC} \)

Gọi \(E\left( {x;y} \right)\) khi đó \(\overrightarrow {BE} \left( {x + 3;y - 6} \right),\,\,\overrightarrow {EC} \left( {1 - x; - 2 - y} \right)\)

Do đó \(\left\{ {\begin{array}{*{20}{c}}{x + 3 = 2\left( {1 - x} \right)}\\{y - 6 = 2\left( { - 2 - y} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x =  - \dfrac{1}{3}}\\{y = \dfrac{2}{3}}\end{array}} \right.\)

Vậy \(E\left( { - \dfrac{1}{3};\dfrac{2}{3}} \right)\)

+ Với $m = 0$: Ta có $\overrightarrow {u\,}  = ( - 2;4)\,\,\,;\overrightarrow {v\,}  = (0;2)$

Vì $\,\dfrac{0}{{ - 2}} \ne \dfrac{2}{4}$ nên hai vectơ $\overrightarrow {u\,} \,;\,\overrightarrow {v\,} \,\,$không cùng phương

+ Với \(m \ne 0\): Ta có $\overrightarrow {u\,} \,;\,\overrightarrow {v\,} \,\,$cùng phương khi và chỉ khi

$\dfrac{{{{\rm{m}}^{\rm{2}}} + m - 2}}{m} = \dfrac{4}{2} \Leftrightarrow {m^2} - m - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m =  - 1}\\{m = 2}\end{array}} \right.$

Vậy với \(m =  - 1\) và \(m = 2\) là các giá trị cần tìm.

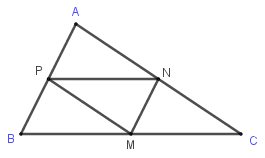
Ta có \(\overrightarrow {MN} \left( { - 3; - 4} \right),\,\,\overrightarrow {PA} \left( {{x_A} - 2;{y_A} + 1} \right)\)

\(\overrightarrow {MN}  = \overrightarrow {PA}  \Leftrightarrow \left\{ \begin{array}{l} - 3 = {x_A} - 2\\ - 4 = {y_A} + 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_A} =  - 1\\{y_A} =  - 5\end{array} \right. \Rightarrow A\left( { - 1; - 5} \right)\)

$N$ là trung điểm $AC$ suy ra \(\left\{ \begin{array}{l}{x_N} = \dfrac{{{x_A} + {x_C}}}{2}\\{y_N} = \dfrac{{{y_A} + {y_C}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 = \dfrac{{ - 1 + {x_C}}}{2}\\ - 3 = \dfrac{{ - 5 + {y_C}}}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} =  - 3\\{y_C} =  - 1\end{array} \right. \Rightarrow C\left( { - 3; - 1} \right)\)

Tương tự $M$ là trung điểm $BC$suy ra \(B\left( {5;3} \right)\)

Giả sử \(\overrightarrow c  = x\overrightarrow a  + y\overrightarrow b \).

Ta có

\(\vec a{\rm{\;}} = (1;3),\vec b{\rm{\;}} = ( - 3;0)\)

\(\begin{array}{l}x.\overrightarrow a  + y\overrightarrow b  = x.\left( {1;3} \right) + y\left( { - 3;0} \right)\\ = \left( {x.1;x.3} \right) + \left( { - 3.y;0.y} \right)\\ = \left( {x;3x} \right) + \left( { - 3y;0} \right)\\ = \left( {x - 3y;3x + 0} \right)\end{array}\)

\(=>x\overrightarrow a  + y\overrightarrow b  = \left( {x - 3y;3x} \right)\)

Suy ra \(\left\{ \begin{array}{l}x - 3y =  - 1\\3x = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = \dfrac{5}{9}\end{array} \right. \) \(\Rightarrow \overrightarrow c  = \dfrac{2}{3}\overrightarrow a  + \dfrac{5}{9}\overrightarrow b \)

$A'$ là điểm đối xứng của $A$ qua $B$ suy ra $B$ là trung điểm của $AA'$

Do đó \(\left\{ \begin{array}{l}{x_B} = \dfrac{{{x_A} + {x_{A'}}}}{2}\\{y_B} = \dfrac{{{y_A} + {y_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 = \dfrac{{3 + {x_{A'}}}}{2}\\2 = \dfrac{{4 + {y_{A'}}}}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} =  - 5\\{y_{A'}} = 0\end{array} \right. \Rightarrow A'\left( { - 5;0} \right)\)

Tương tự \(B'\left( {9;0} \right),\,\,C'\left( {2;7} \right)\)

Trọng tâm của tam giác \(ABC\) và \(A'B'C'\) có cùng tọa độ là \(\left( {2;\dfrac{7}{3}} \right)\)

Vậy các đáp án B, C, D đều đúng.

Vì $I$ là trọng tâm tam giác \(ABC\) nên

${x_I} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} \Rightarrow {x_C} = 3{x_I} - {x_A} - {x_B} = 1$

${y_I} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3} \Rightarrow {y_C} = 3{y_I} - {y_A} - {y_B} =  - 4$

Suy ra \(C\left( {1; - 4} \right)\)

Điểm $O$ là tâm của hình bình hành \(ABCD\) suy ra $O$ là trung điểm $AC$ do đó

${x_O} = \dfrac{{{x_A} + {x_C}}}{2} = 2,\,\,{y_O} = \dfrac{{{y_A} + {y_C}}}{2} =  - \dfrac{5}{2} \Rightarrow O\left( {2; - \dfrac{5}{2}} \right)$

$G$ là trọng tâm tam giác suy ra

${x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} = \dfrac{{2 - 1 - 3}}{3} =  - \dfrac{2}{3}$ và ${y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{2} = \dfrac{{1 - 2 + 2}}{3} = \dfrac{1}{3}$

Vậy \(G\left( { - \dfrac{2}{3};\dfrac{1}{3}} \right)\)

Gọi \(M\left( {x;y} \right)\), ta có  \(\overrightarrow {MA} \left( { - 4 - x; - y} \right),\,\,\overrightarrow {MB} \left( { - x;3 - y} \right),\,\,\overrightarrow {MC} \left( {2 - x;1 - y} \right)\)

Suy ra  $\overrightarrow {MA}  + 2\overrightarrow {MB}  + 3\overrightarrow {MC}  = \left( { - 6x + 2; - 6y + 9} \right)$

Do đó \(\overrightarrow {MA}  + 2\overrightarrow {MB}  + 3\overrightarrow {MC}  = \overrightarrow 0  \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ - 6x + 2 = 0}\\{ - 6y + 9 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \dfrac{1}{3}}\\{y = \dfrac{3}{2}}\end{array}} \right.\)

Vậy \(M\left( {\dfrac{1}{3};\dfrac{3}{2}} \right)\)

Ta có \(3\overrightarrow u  + 2\overrightarrow a  + 3\overrightarrow b  = 3\overrightarrow c  \Leftrightarrow \overrightarrow u  =  - \dfrac{2}{3}\overrightarrow a  - \overrightarrow b  + \overrightarrow c \)

Suy ra \(\overrightarrow u  = \left( { - \dfrac{2}{3} + 3 - 1; - \dfrac{4}{3} - 4 + 3} \right) = \left( {\dfrac{4}{3}; - \dfrac{7}{3}} \right)\)

Ta có $2\overrightarrow {a\,}  = (6;4)\,\,\overrightarrow {\,b}  = ( - 1;5)\,$suy ra $\overrightarrow {k\,}  = \left( {6 - 1;4 + 5} \right) = \left( {5;9} \right)$;

$ - \overrightarrow {a\,}  = ( - 3; - 2),\,\,2\overrightarrow {b\,}  = ( - 2;10)$ và $5\overrightarrow {c\,} \, = ( - 10; - 25)\,$suy ra

$\overrightarrow l  = \left( { - 3 - 2 - 10; - 2 + 10 - 25} \right) = \left( { - 15; - 17} \right)$

Kẻ \(BH \bot AD \Rightarrow BH = 3;\)\(AB = \dfrac{{BH}}{{\sin {{60}^0}}} = \dfrac{3}{{\sqrt 3 /2}} = 2\sqrt 3 ;\)\(AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {12 - 9}  = \sqrt 3 ,\)

Do đó:

$\begin{array}{l}A(0;0)\,\,\,;\,B(\sqrt 3 ;3),C(4 + \sqrt 3 ;3)\,\,\,D(4;0)\\\overrightarrow {AB}  = \left( {\sqrt 3 ;3} \right),\overrightarrow {BC}  = (4;0),\overrightarrow {CD}  = \left( { - \sqrt 3 ; - 3} \right)\\\overrightarrow {AC}  = \left( {4 + \sqrt 3 ;3} \right)\end{array}$

Từ giả thiết ta xác định được hình thoi trên mặt phẳng tọa độ \(Oxy\)

Gọi $I$ là tâm hình thoi ta có \(BI = AB\sin \widehat {BAI} = a\sin {30^0} = \dfrac{a}{2}\)

\(AI = \sqrt {A{B^2} - B{I^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Suy ra \(A\left( {0;0} \right),\,\,B\left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2}} \right),\,\)\(\,C\left( {a\sqrt 3 ;0} \right),\,\,D\left( {\dfrac{{a\sqrt 3 }}{2}; - \dfrac{a}{2}} \right)\)

Từ giả thiết ta xác định được hình vuông trên mặt phẳng tọa độ

Vì điểm \(A(1;3)\) suy ra \(AB = 3,\,\,OB = 1\)

Do đó \(B\left( {1;0} \right),\,\,C\left( {4;0} \right),\,\,D\left( {4;3} \right)\)

Vậy \(\overrightarrow {AB} \left( {0; - 3} \right),\,\,\overrightarrow {BC} \left( {3;0} \right)\)

Theo quy tắc ba điểm ta có

\(\begin{array}{l}\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \left( {\overrightarrow {OP}  + \overrightarrow {PA} } \right) + \left( {\overrightarrow {OM}  + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON}  + \overrightarrow {NC} } \right)\\ = \left( {\overrightarrow {OM}  + \overrightarrow {ON}  + \overrightarrow {OP} } \right) + \overrightarrow {PA}  + \overrightarrow {MB}  + \overrightarrow {NC} \\ = \left( {\overrightarrow {OM}  + \overrightarrow {ON}  + \overrightarrow {OP} } \right) - \left( {\overrightarrow {BM}  + \overrightarrow {CN}  + \overrightarrow {AP} } \right)\end{array}\)

Vì \(PN,\,MN\) là đường trung bình của tam giác \(ABC\) nên

\(PN//BM,\,\,MN//BP\) suy ra tứ giác \(BMNP\) là hình bình hành

\( \Rightarrow \overrightarrow {BM}  = \overrightarrow {PN} \)

\(N\) là trung điểm của \(AC \Rightarrow \overrightarrow {CN}  = \overrightarrow {NA} \)

Do đó theo quy tắc ba điểm ta có

\(\begin{array}{l}\overrightarrow {BM}  + \overrightarrow {CN}  + \overrightarrow {AP}  = \left( {\overrightarrow {PN}  + \overrightarrow {NA} } \right) + \overrightarrow {AP} \\ = \overrightarrow {PA}  + \overrightarrow {AP}  = \overrightarrow 0 \end{array}\)

Do đó \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow {OM}  + \overrightarrow {ON}  + \overrightarrow {OP} \)

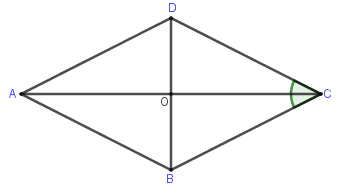
Ta có \(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\) (quy tắc hình bình hành)

Xét tam giác \(BCD\) có \(CD = CB = a\) và góc \(\widehat {BCD} = {60^0}\) nên tam giác \(BCD\) đều cạnh \(a\)

Xét tam giác \(DOC\) có \(\widehat O = {90^0}\) và \(DC = a,DO = \dfrac{1}{2}DB = \dfrac{a}{2}\) nên \(CO = \sqrt {D{C^2} - D{O^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Do đó \(AC = 2OC = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \) hay \(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = a\sqrt 3 \) nên A đúng.

Lại có:

\(\overrightarrow {OB}  - \overrightarrow {DC}  = \overrightarrow {DO}  - \overrightarrow {DC}  = \overrightarrow {CO} \) nên \(\left| {\overrightarrow {OB}  - \overrightarrow {DC} } \right| = \left| {\overrightarrow {CO} } \right| = CO = \dfrac{{a\sqrt 3 }}{2}\)

\(\left| {\overrightarrow {OB}  - \overrightarrow {DC} } \right| = \left| {\overrightarrow {CO} } \right| = \,\,\dfrac{{a\sqrt 3 }}{2} \ne \dfrac{{a\sqrt 3 }}{4}\) nên B sai.

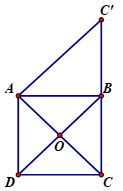
Theo quy tắc phép trừ ta có

\(\overrightarrow u  = \left( {\overrightarrow {MA}  - \overrightarrow {MC} } \right) + \left( {\overrightarrow {MB}  - \overrightarrow {MD} } \right) = \overrightarrow {CA}  + \overrightarrow {DB} \)

Suy ra \(\overrightarrow u \) không phụ thuộc vị trí điểm \(M\).

Qua \(A\) kẻ đường thẳng song song với \(DB\) cắt \(BC\) tại \(C'\).

Khi đó tứ giác \(ADBC'\) là hình bình hành (vì có cặp cạnh đối song song) suy ra \(\overrightarrow {DB}  = \overrightarrow {AC'} \)

Do đó \(\overrightarrow u  = \overrightarrow {CA}  + \overrightarrow {AC'}  = \overrightarrow {CC'} \)

=> \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {CC'} } \right| =CC'= BC + BC' \)

Mà ta có $BC'=AD=a$ (do $ADBC'$ là hình bình hành) và $BC=a$ (gt)

Vậy \(\left| {\overrightarrow u } \right| = a + a = 2a\)

Gọi \(D\) là điểm sao cho tứ giác \(ABDC\) là hình bình hành.

Khi đó theo quy tắc hình bình hành ta có \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)

Vì tam giác \(ABC\) vuông ở \(A\) nên tứ giác \(ABDC\) là hình chữ nhật suy ra \(AD = BC = a\sqrt 5 \)

Vậy \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 5 \)

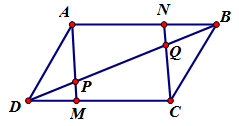
Ta có \(DM = BN \Rightarrow AN = MC\), mặt khác \(AN\) song song với \(MC\) do đó tứ giác \(ANCM\) là hình bình hành

Suy ra \(\overrightarrow {AM}  = \overrightarrow {NC} \).

Xét tam giác \(\Delta DMP\) và \(\Delta BNQ\) ta có \(DM = NB\) (giả thiết), \(\widehat {PDM} = \widehat {QBN}\) (so le trong)

Mặt khác \(\widehat {DMP} = \widehat {APB}\) (đối đỉnh) và \(\widehat {APQ} = \widehat {NQB}\) (hai góc đồng vị) suy ra \(\widehat {DMP} = \widehat {BNQ}\).

Do đó \(\Delta DMP = \Delta BNQ\) (c.g.c) suy ra \(DP = QB\).

Dễ thấy \(\overrightarrow {DP} ,\,\,\overrightarrow {QB} \) cùng hướng vì vậy \(\overrightarrow {DP}  = \overrightarrow {QB} \).

Ta có \(\overrightarrow {B'B}  = \overrightarrow {AG} \) suy ra \(B'B = AG\).

Dễ thấy \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \) cùng hướng (1).

Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(IG = \dfrac{1}{2}AG\), \(J\) là trung điểm \(BB'\) suy ra \(BJ = \dfrac{1}{2}BB'\)

Vì vậy \(BJ = IG\) (2)

Từ (1) và (2) ta có \(\overrightarrow {BJ}  = \overrightarrow {IG} \).

Ta có $\left| {\overrightarrow {AB} } \right| = AB = a$

Gọi $M$ là trung điểm của \(BC\)\( \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{a}{2}\)

Tam giác \(ABM\) vuông tại \(M\) nên \(AM = \sqrt {A{B^2} - B{M^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Ta có \(\left| {\overrightarrow {AG} } \right| = AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)

Mà \(I\) là trung điểm của \(AG\) nên \(MI = AG = \dfrac{{a\sqrt 3 }}{3}\)

\(\left| {\overrightarrow {BI} } \right| = BI = \sqrt {B{M^2} + M{I^2}}  = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt {21} }}{6}\)