Tam giác $ABC$ vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Gọi \(r\) là bán kính đường tròn nội tiếp tam giác $ABC$. Khi đó tỉ số \(\dfrac{R}{r}\) bằng
Ta có \(R = \dfrac{{abc}}{{4S}}\), \(r = \dfrac{S}{p}\)
Vì tam giác $ABC$ vuông cân tại \(A\) nên \(b = c\) và \(a = \sqrt {{b^2} + {c^2}} = b\sqrt 2 \)
Xét tỉ số \(\dfrac{R}{r} = \dfrac{{abc.p}}{{4{S^2}}}\)\( = \dfrac{{abc.\dfrac{{a + b + c}}{2}}}{{4.\dfrac{1}{4}.{{\left( {b.c} \right)}^2}}}\)\( = \dfrac{{a\left( {a + 2b} \right)}}{{2{b^2}}}\)\( = \dfrac{{2{b^2}\left( {1 + \sqrt 2 } \right)}}{{2{b^2}}}\)\( = 1 + \sqrt 2 \).
Trên nóc một tòa nhà có cột ăng-ten cao \(5\,{\rm{m}}\). Từ vị trí quan sát \(A\) cao \(7\,{\rm{m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là:

Ta có chiều cao của tòa nhà chính là đoạn \(BH\).
Mà \(BH = CD + DH\)\( = CD + 7\).
Xét tam giác \(ACD\) vuông tại \(D\) có \(AC = \dfrac{{CD}}{{\sin 40^\circ }}\)
Xét tam giác \(ABD\) vuông tại \(D\) có \(AB = \dfrac{{5 + CD}}{{\sin 50^\circ }}\)
Xét tam giác \(ABC\) có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)
\( \Leftrightarrow \left( {\dfrac{1}{{{{\sin }^2}50^\circ }} + \dfrac{1}{{{{\sin }^2}40^\circ }} - \dfrac{{2\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)C{D^2} + \left( {\dfrac{{10}}{{{{\sin }^2}50^\circ }} - \dfrac{{10\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)CD + \dfrac{{25}}{{{{\sin }^2}50^\circ }} - 25 = 0\)\( \Leftrightarrow CD \approx 11,9\)
\( \Rightarrow BC \approx 7 + 11,9\)\( \approx 18,9\) (m).
Vậy tòa nhà cao \(18,9{\rm{ m}}\).
Giá trị của $\tan {180^0}$ bằng:
Ta có: \(\tan {180^0} = 0\)
Cho tam giác ABC, có BC = a, CA = b, AB = c. Mệnh đề nào sau đây đúng?
Nếu \(\cos A > 0\) thì góc A nhọn hay \({b^2} + {c^2} - {a^2} > 0\) thì góc A nhọn.
Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C = - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.
Áp dụng định lí cosin trong tam giác \(ABC\) ta có:
\({c^2} = {a^2} + {b^2} - 2a.b.\cos C\)\( \Rightarrow 81 = 25 + {b^2} - 2.5.b.\left( { - \dfrac{1}{{10}}} \right)\)\( \Leftrightarrow {b^2} - b - 56 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}b = 7\\b = - 8\end{array} \right.\)
Ta nhận được \(b = 7({\rm{cm}})\)
Diện tích tam giác \(ABC\) là \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)\( = \sqrt {\dfrac{{21}}{2}\left( {\dfrac{{21}}{2} - 5} \right)\left( {\dfrac{{21}}{2} - 7} \right)\left( {\dfrac{{21}}{2} - 9} \right)} \)\( = \dfrac{{21\sqrt {11} }}{4}({\rm{c}}{{\rm{m}}^2})\)
Độ dài đường cao \({h_a} = \dfrac{{2S}}{a}\)\( = \dfrac{{\dfrac{{21\sqrt {11} }}{2}}}{5}\)\( = \dfrac{{21\sqrt {11} }}{{10}}({\rm{cm}})\)
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) thỏa mãn \(MO = 3R\). Một đường kính \(AB\) thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức \(S = MA + MB\).
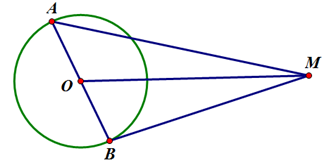
Gọi \(\widehat {MOA} = \alpha \Rightarrow \widehat {MOB} = 180^\circ - \alpha \).
Ta có \(MA = \sqrt {M{O^2} + A{O^2} - 2MO.AO.\cos \alpha } = \sqrt {9{R^2} + {R^2} - 6{R^2}\cos \alpha } = R\sqrt {10 - 6\cos \alpha } \).
\(MB = \sqrt {M{O^2} + B{O^2} - 2MO.BO.\cos \left( {180^\circ - \alpha } \right)} = \sqrt {9{R^2} + {R^2} + 6{R^2}\cos \alpha } = R\sqrt {10 + 6\cos \alpha } \).
Xét \(C = \sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } \) \( \Rightarrow {C^2} = 20 + 2\sqrt {100 - 36{{\cos }^2}\alpha } \ge 20 + 2\sqrt {100 - 36} = 36\).
Suy ra \(C \ge 6\). Dấu xẩy ra khi ${\cos ^2}\alpha = 1 \Leftrightarrow \left[ \begin{array}{l}\cos \alpha = 1\\\cos \alpha = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = 0^\circ \\\alpha = 180^\circ \end{array} \right.$.
Ta có $S = MA + MB = R\left( {\sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } } \right) \ge 6R$.
Suy ra \(\min S = 6R\) khi và chỉ khỉ \(A\), \(O\), \(B\), \(M\) thẳng hàng.
Từ một miếng tôn có hình dạng là nửa đường tròn bán kính $1\;{\rm{m}}$, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?


Xét đường tròn bán kính $1$, ta cắt trên đó một hình chữ nhật $ABCD$.
Khi đó ${S_{ABCD}} = \dfrac{1}{2}AC.BD.\sin \alpha $$ = 2\sin \alpha \le 2$.
Dấu bằng xảy ra khi và chỉ khi $\alpha = 90^\circ $.
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng $1$.
Cho $\cot x = \dfrac{3}{4}$ và góc $x$ thỏa mãn ${90^0} < x < {180^0}$. Khi đó:
$\cot x = \dfrac{3}{4} \Leftrightarrow \tan \,x=\dfrac{1}{\cot x} = \dfrac{4}{3}$
=>Phương án A sai
$1 + {\cot ^2}x = \dfrac{1}{{{{\sin }^2}x}}$ $ \Leftrightarrow 1 + {\left( {\dfrac{3}{4}} \right)^2} = \dfrac{1}{{{{\sin }^2}x}}$ $ \Leftrightarrow {\sin ^2}x = \dfrac{{16}}{{25}} $ $\Leftrightarrow \sin \,x = \pm \dfrac{4}{5}$.
Mà ${90^0} < x < {180^0} \Rightarrow \sin \,x >0\Rightarrow \sin \,x = \dfrac{4}{5}$
=> Phương án D sai, C đúng.
Vì ${\sin ^2}x = \dfrac{{16}}{{25}} \Rightarrow {\cos ^2}x=1-{\sin ^2}x = \dfrac{9}{{25}}$ $ \Leftrightarrow \cos x= \pm \dfrac{3}{5}$
Mà ${90^0} < x < {180^0} \Rightarrow \cos x <0\Rightarrow \cos x = - \dfrac{3}{5}$
=>Phương án B sai.
Biết $\sin \alpha = \dfrac{{\sqrt {2017} + 1}}{{2018}},$ $90^\circ < \alpha < 180^\circ $. Tính giá trị của biểu thức $M = \cot \alpha + \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}$.
$M = \cot \alpha + \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}$\( = \dfrac{{\cos \alpha }}{{\sin \alpha }} + \dfrac{{\sin \alpha }}{{1 + \cos \alpha }}\) \( = \dfrac{{1 + \cos \alpha }}{{\sin \alpha \left( {1 + \cos \alpha } \right)}}\) \( = \dfrac{1}{{\sin \alpha }}\) \( = \dfrac{{2018}}{{\sqrt {2017} + 1}}\).
Cho hình thang cân \(ABCD\) có đáy nhỏ \(AB\), đáy lớn \(CD\). Biết \(AB = AD\) và \(\tan \widehat {BDC} = \dfrac{3}{4}\). Tính $\cos \widehat {BAD}$.
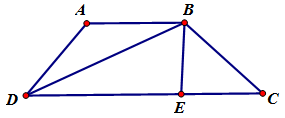
Gọi $E$ là hình chiếu vuông góc của \(B\) trên $DC$. Đặt $AB = AD = BC = x$.
Ta có \(EC = \dfrac{{DC - x}}{2}\) \(\left( 1 \right)\).
Trong tam giác vuông \(BDE\) ta có: \(\tan \widehat {BDC} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(\dfrac{{BE}}{{ED}} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(BE = \dfrac{3}{4}ED\)
\( \Leftrightarrow \) \(BE = \dfrac{3}{4}\left( {DC - \dfrac{{DC - x}}{2}} \right)\)\( = \dfrac{3}{8}\left( {DC + x} \right)\) \(\left( 2 \right)\).
Trong tam giác vuông \(BEC\) ta có \(B{C^2} = E{C^2} + B{E^2}\) \(\left( 3 \right)\).
Thay \(\left( 1 \right)\), \(\left( 2 \right)\) vào \(\left( 3 \right)\) biến đổi ta được: \(39{x^2} + 14DC.\,x - 25D{C^2} = 0\) \( \Leftrightarrow \) \(x = \dfrac{{25}}{{39}}DC\) hay \(DC = \dfrac{{39}}{{25}}x\). Khi đó \(EC = \dfrac{7}{{25}}x\).
Mặt khác: $\cos \widehat {BAD}$\( = - \cos \widehat {BCE}\)\( = - \dfrac{{EC}}{{BC}} = - \dfrac{7}{{25}}\)
Nếu $\sin x = \dfrac{4}{5}$ thì giá trị của $\cos 4x = ?$
$\cos 4x = 2{\cos ^2}2x - 1$ $ = 2.{\left( {1 - 2{{\sin }^2}x} \right)^2} - 1$ $ = 2{\left( {1 - 2.{{\left( {\dfrac{4}{5}} \right)}^2}} \right)^2} - 1$ $ = - \dfrac{{527}}{{625}}$
Nếu $\sin a - \cos a = \dfrac{1}{5}\,\,\left( {{{135}^0} < a < {{180}^0}} \right)$ thì giá trị đúng của $\tan 2a$ là:
$\sin a - \cos a = \dfrac{1}{5}\, \Rightarrow {\left( {\sin a - \cos a} \right)^2} = \dfrac{1}{{25}} \Leftrightarrow {\sin ^2}a - 2\sin a\cos a + {\cos ^2}a = \dfrac{1}{{25}} \Leftrightarrow 1 - \sin 2a = \dfrac{1}{{25}} \Leftrightarrow \sin 2a = \dfrac{{24}}{{25}}$
Ta có: ${\sin ^2}2a + {\cos ^2}2a = 1 \Rightarrow {\left( {\dfrac{{24}}{{25}}} \right)^2} + {\cos ^2}2a = 1 \Leftrightarrow {\cos ^2}2a = \dfrac{{49}}{{625}} \Leftrightarrow \cos 2a = \pm \dfrac{7}{{25}}$
Mà ${135^0} < a < {180^0} \Leftrightarrow {270^0} < 2a < {360^0} \Rightarrow \cos 2a > 0 \Rightarrow \cos 2a = \dfrac{7}{{25}}$
$\tan 2a = \dfrac{{\sin 2a}}{{\cos 2a}} = \dfrac{{\dfrac{{24}}{{25}}}}{{\dfrac{7}{{25}}}} = \dfrac{{24}}{7}$
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \({60^0}\). Tàu thứ nhất chạy với tốc độ \(30\,km/h\), tàu thứ hai chạy với tốc độ \(40\,km/h\). Hỏi sau \(2\) giờ hai tàu cách nhau bao nhiêu \(km\)?

Ta có: Sau \(2h\) quãng đường tàu thứ nhất chạy được là: \({S_1} = 30.2 = 60\,km.\)
Sau \(2h\) quãng đường tàu thứ hai chạy được là: \({S_2} = 40.2 = 80\,km.\)
Vậy: sau \(2h\) hai tàu cách nhau là: \(S = \sqrt {{S_1}^2 + {S_2}^2 - 2{S_1}.{S_2}.\cos {{60}^0}} = 20\sqrt {13} .\)
Xác định dạng của tam giác $ABC$ biết rằng $S = \dfrac{{\sqrt 3 }}{{36}}{\left( {a + b + c} \right)^2}$
Theo công thức He-rong ta có
$\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{\sqrt 3 }}{9}{p^2} \Leftrightarrow \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) = \dfrac{1}{{27}}{p^3}$
Theo bất đẳng thức Cauchy ta có $\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \le \dfrac{{{{\left( {p - a + p - b + p - c} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - \left( {a + b + c} \right)} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - 2p} \right)}^3}}}{{27}} = \dfrac{{{p^3}}}{{27}}$
Đẳng thức xảy ra khi a = b = c.
Khi đó tam giác $ABC$ đều.
Tìm bán kính đường tròn ngoại tiếp tam giác $ABC $ biết $ b = 7cm,\,\,c = 5 cm,\,\,{\mathop{\rm cosA}\nolimits} = \dfrac{3}{5}$.
Theo định lí cosin ta có ${a^2} = {b^2} + {c^2} - 2bc\cos A = {7^2} + {5^2} - 2.7.5.\dfrac{3}{5} = 32 \Rightarrow a = 4\sqrt 2 $
Từ công thức ${\sin ^2}A + {\cos ^2}A = 1 \Rightarrow {\mathop{\rm sinA}\nolimits} = \dfrac{4}{5}$
Theo định lí sin ta có $\dfrac{a}{{\sin A}} = 2R \Rightarrow R = \dfrac{a}{{2\sin A}} = \dfrac{{4\sqrt 2 }}{{2.\dfrac{4}{5}}} = \dfrac{{5\sqrt 2 }}{2}$.
Xác định hình dạng tam giác $ABC$ biết $\left\{ \begin{array}{l}\dfrac{{{b^3} + {c^3} - {a^3}}}{{b + c - a}} = {a^2}\\a = 2b\cos C\end{array} \right.$
Theo định lí cosin ta có ${\mathop{\rm cosC}\nolimits} = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$, thay vào đẳng thức thứ hai của hệ trên ta có
$a = 2b{\mathop{\rm cosC}\nolimits} = 2b.\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \Rightarrow {a^2} = {a^2} + {b^2} - {c^2} \Leftrightarrow {b^2} - {c^2} = 0 \Leftrightarrow {b^2} = {c^2} \Rightarrow b = c$
Thay b = c vào hệ thức thứ nhất ta có $\dfrac{{2{b^3} - {a^3}}}{{2b - a}} = {a^2} \Leftrightarrow 2{b^3} - {a^3} = 2b{a^2} - {a^3} \Leftrightarrow {b^2} = {a^2} \Rightarrow a = b$
Do đó a = b = c. Vậy tam giác $ABC$ đều.

