Ứng dụng của hệ phương trình bậc nhất ba ẩn
Sách kết nối tri thức với cuộc sống
Một nhà máy có ba bộ phận cắt, may, đóng gói để sản xuất ba loại sản phẩm: áo thun, áo sơ mi, áo khoác. Thời gian (tính bằng phút) của mỗi bộ phận để sản xuất 10 cái áo mỗi loại được thể hiện trong bảng sau:
|
Bộ phận |
Thời gian (tính bằng phút) để sản xuất 10 cái |
||
|
Áo thun |
Áo sơ mi |
Áo khoác |
|
|
Cắt |
9 |
12 |
15 |
|
May |
22 |
24 |
28 |
|
Đóng gói |
6 |
8 |
8 |
Gọi số lượng áo thun, áo sơ mi, áo khoác cần sản xuất để nhà máy hoạt động hết công suất lần lượt là x, y, z.
Giá trị biểu thức \(D = 5x - z + 3y\) là:
Giá trị biểu thức \(D = 5x - z + 3y\) là:
Đổi: 80 giờ = 4800 phút, 160 giờ = 9600 phút, 48 giờ = 2880 phút.
Nhà máy hoạt động hết công suất nghĩa là sử dụng được hết thời gian lao động tối đa.
Gọi số lượng áo thun, áo sơ mi, áo khoác cần sản xuất để nhà máy hoạt động hết công suất lần lượt là x, y, z (x, y, z nguyên dương).
Dựa vào bảng trên ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{9x + 12y + 15z = 4800}\\{22x + 24y + 28z = 9600}\\{6x + 8y + 8z = 2880}\end{array}} \right.\)
Giải hệ này ta được x = 80, y = 140, z = 160.
Giá trị biểu thức: \(D = 5.80 - 140 + 3.160 = 740\).
Nhân dịp kỉ niệm ngày thành lập Đoàn Thanh niên Cộng sản Hồ Chí Minh, một trường Trung học phổ thông đã tổ chức cho học sinh tham gia các trò chơi. Ban tổ chức đã chọn 100 bạn và chia thành ba nhóm A, B, C để tham gia trò chơi thứ nhất. Sau khi trò chơi kết thúc, ban tổ chức chuyển \(\dfrac{1}{3}\) số bạn ở nhóm A sang nhóm B; \(\dfrac{1}{2}\) số bạn ở nhóm B sang nhóm C; số bạn chuyển từ nhóm C sang nhóm A và B đều bằng \(\dfrac{1}{3}\) số bạn ở nhóm C ban đầu. Tuy nhiên, người ta nhận thấy số bạn ở mỗi nhóm là không đổi qua hai trò chơi.
Ban tổ chức đã chia nhóm B:
bạn
Ban tổ chức đã chia nhóm B:
bạn
Gọi số bạn trong mỗi nhóm A, B, C lần lượt là x, y, z (\(x,y,z \in {\mathbb{N}^*}\))(bạn)
Theo đề bài ta có: x + y + z = 100 (1).
- Số bạn ở nhóm A sau khi chuyển là: \(x - \dfrac{1}{3}x + \dfrac{1}{3}z\)
- Số bạn ở nhóm B sau khi chuyển là: \(y - \dfrac{1}{2}y + \dfrac{1}{3}x + \dfrac{1}{3}z\)
Vì số bạn ở mỗi nhóm là không đổi qua hai trò chơi nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{x - \dfrac{1}{3}x + \dfrac{1}{3}z = x}\\{y - \dfrac{1}{2}y + \dfrac{1}{3}x + \dfrac{1}{3}z = y}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x - z = 0}\\{2x - 3y + 2z = 0}\end{array}} \right.(2)\)
Từ (1), (2) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{x - z = 0}\\{2x - 3y + 2z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 30, y = 40, z = 30.
Ban tổ chức đã chia nhóm B 40 bạn.
Nhân dịp kỉ niệm ngày thành lập Đoàn Thanh niên Cộng sản Hồ Chí Minh, một trường Trung học phổ thông đã tổ chức cho học sinh tham gia các trò chơi. Ban tổ chức đã chọn 100 bạn và chia thành ba nhóm A, B, C để tham gia trò chơi thứ nhất. Sau khi trò chơi kết thúc, ban tổ chức chuyển \(\dfrac{1}{3}\) số bạn ở nhóm A sang nhóm B; \(\dfrac{1}{2}\) số bạn ở nhóm B sang nhóm C; số bạn chuyển từ nhóm C sang nhóm A và B đều bằng \(\dfrac{1}{3}\) số bạn ở nhóm C ban đầu. Tuy nhiên, người ta nhận thấy số bạn ở mỗi nhóm là không đổi qua hai trò chơi.
Ban tổ chức đã chia nhóm C:
bạn
Ban tổ chức đã chia nhóm C:
bạn
Gọi số bạn trong mỗi nhóm A, B, C lần lượt là x, y, z (\(x,y,z \in {\mathbb{N}^*}\))(bạn)
Theo đề bài ta có: x + y + z = 100 (1).
- Số bạn ở nhóm A sau khi chuyển là: \(x - \dfrac{1}{3}x + \dfrac{1}{3}z\)
- Số bạn ở nhóm B sau khi chuyển là: \(y - \dfrac{1}{2}y + \dfrac{1}{3}x + \dfrac{1}{3}z\)
Vì số bạn ở mỗi nhóm là không đổi qua hai trò chơi nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{x - \dfrac{1}{3}x + \dfrac{1}{3}z = x}\\{y - \dfrac{1}{2}y + \dfrac{1}{3}x + \dfrac{1}{3}z = y}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x - z = 0}\\{2x - 3y + 2z = 0}\end{array}} \right.(2)\)
Từ (1), (2) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{x - z = 0}\\{2x - 3y + 2z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 30, y = 40, z = 30.
Ban tổ chức đã chia nhóm C 30 bạn.
Cường độ dòng điện qua điện trở và các bóng đèn Đ1 , Đ2 là:
Gọi cường độ dòng điện qua điện trở R và các bóng đèn Đ1, Đ2 lần lượt là I, I1, I2 (ampe).
Cường độ dòng điện của đoạn mạch mắc song song là: I1 + I2.
Ta có: I = I1 + I2 hay I – I1 – I2 = 0 (1).
Hiệu điện thế ở đoạn mạch mắc song song là: U' = R1 . I1 = R2 . I2 nên
24 . I1 = 12 . I2 hay 2I1 – I2 = 0 (2).
Hiệu điện thế của đoạn mạch là: U = UR + U' nên
24 = R . I + R1 . I1 suy ra 3I + 24I1 = 24, hay I + 8I1 = 8 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I - {I_1} - {I_2} = 0}\\{2{I_1} - {I_2} = 0}\\{I + 8{I_1} = 8}\end{array}} \right.\)
Giải hệ phương trình, ta được:
\(I = \dfrac{{24}}{{11}}\left( A \right),\,{I_1} = \dfrac{8}{{11}}\left( A \right),\,{I_2} = \dfrac{{16}}{{11}}\left( A \right).\)
Điện trở của mỗi bóng đèn Đ1 và Đ2 là:
Điện trở của Đ1 là: R1 = \(\dfrac{{{{12}^2}}}{6}\)=24(Ω).
Điện trở của Đ2 là: R2 = \(\dfrac{{{{12}^2}}}{{12}}\)=12(Ω).
Ba lớp 10A, 10B, 10C trồng được 164 cây bạch đàn và 316 cây thông. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 2 cây thông; mỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 3 cây thông; mỗi học sinh lớp 10C trồng được 5 cây thông. Biết số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C.
Tổng số học sinh của ba lớp 10A, 10B, 10C là:
Tổng số học sinh của ba lớp 10A, 10B, 10C là:
Gọi số học sinh của ba lớp 10A, 10B, 10C lần lượt là x, y, z (học sinh) (x, y, z ∈ ℕ*).
Theo đề bài ta có:
- Số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C, suy ra:
\(x = \;\dfrac{{y + z}}{2} \Rightarrow 2x-y-z = 0{\rm{ }}\left( 1 \right).\)
- Số cây bạch đàn mỗi học sinh lớp 10A, 10B trồng được lần lượt là: 3, 2. Suy ra:
\(3x + 2y = 164{\rm{ }}\left( 2 \right).\)
- Số cây thông mỗi học sinh lớp 10A, 10B, 10C trồng được lần lượt là: 2, 3, 5. Suy ra:
\(2x + 3y + 5z\; = 316{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x - y - z = 0}\\{3x + 2y = 164}\\{2x + 3y + 5z = 316}\end{array}} \right.\)
Giải hệ này ta được x = 32, y = 34, z = 30 (thoả mãn điều kiện).
Vậy số học sinh của ba lớp 10A, 10B, 10C lần lượt là 32, 34, 30 học sinh.
=>Tổng số học sinh của ba lớp là: \(32 + 34 + 30 = 96\)(học sinh).
Một giáo viên dạy Hoá tạo 1000 g dung dịch HCl 25% từ ba loại dung dịch HCl có nồng độ lần lượt là 10%, 20% và 30%. Biết rằng lượng HCl có trong dung dịch 10% bằng \(\dfrac{1}{4}\) lượng HCl có trong dung dịch 20%. Gọi khối lượng dung dịch mỗi loại có nồng độ 10%, 20% và 30% lần lượt là x, y, z.
Giá trị biểu thức \(P = x - 2y + z\) là:
Giá trị biểu thức \(P = x - 2y + z\) là:
Gọi khối lượng dung dịch HCl có nồng độ 10%, 20% và 30% lần lượt là x, y, z (g).
Theo đề bài ta có: x + y + z = 1000 (1).
Vì dung dịch mới có nồng độ 25% nên ta có:
\(\dfrac{{10\% x + 20\% y + 30\% z}}{{1000}} = 25\% \)
\(\begin{array}{l} \Leftrightarrow 10x + 20y + 30z = 25\,\,000\\ \Leftrightarrow x + 2y + 3z = 2500\,\,(2)\end{array}\)
Lượng HCl có trong dung dịch 10% bằng lượng HCl có trong dung dịch 20%.
\( \Rightarrow 10\% x = \dfrac{1}{4}20\% y \Leftrightarrow 2x - y = 0\left( 3 \right)\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 1000}\\{x + 2y + 3z = 2500}\\{2x - y = 0}\end{array}} \right.\)
Giải hệ này ta được x = 125, y = 250, z = 625.
=> khối lượng dung dịch HCl có nồng độ 10%, 20% và 30% lần lượt là 125 g, 250 g, 625 g.
Vậy: \(P = x - 2y + z = 125 - 2.250 + 625 = 250\)
Một ngân hàng muốn đầu tư số tiền tín dụng là 100 tỉ đồng thu được vào ba nguồn: mua trái phiếu với mức sinh lời 8%/năm, cho vay thu lãi suất 10%/năm và đầu tư bất động sản với mức sinh lời 12%/năm. Theo điều kiện của quỹ tín dụng đề ra là tổng số tiền đầu tư vào trái phiếu và cho vay phải gấp ba lần số tiền đầu tư vào bất động sản. Ngân hàng muốn thu được mức thu nhập 9,6 tỉ đồng hằng năm, gọi số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là x, y, z (tỉ đồng).
Giá trị biểu thức: \(P = 2x + y - 2z\) là:
Giá trị biểu thức: \(P = 2x + y - 2z\) là:
Gọi số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là x, y, z (tỉ đồng).
Theo đề bài ta có: x + y + z = 100 (1).
Tổng số tiền đầu tư vào trái phiếu và cho vay gấp ba lần số tiền đầu tư vào bất động sản, do đó:
x + y = 3z hay x + y – 3z = 0 (2).
Lãi suất cho ba khoản đầu tư lần lượt là 8%, 10%, 12% và tổng số tiền lãi thu được là 9,6 tỉ đồng nên:
8%x + 10%y + 12%z = 9,6
suy ra 8x + 10y + 12z = 960 hay 4x + 5y + 6z = 480 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{x + y - 3z = 0}\\{4x + 5y + 6z = 480}\end{array}} \right.\)
Giải hệ này ta được x = 45, y = 30, z = 25.
Vậy số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là 45 tỉ đồng, 30 tỉ đồng và 25 tỉ đồng.
=>\(P = 2.45 + 30 - 2.25 = 70\)
Cân bằng phương trình sau:
\(xKCl{O_3}\;\mathop \to \limits^{{t^o}} \;yKCl + z{O_2}\)
Giá trị biểu thức: \(A = 5x - y + 3z\) là:
Giá trị biểu thức: \(A = 5x - y + 3z\) là:
Theo định luật bảo toàn nguyên tố với K, Cl và O, ta có:
x = y hay x – y = 0 (1)
3x = 2z hay 3x – 2z = 0 (2)
Từ (1) và (2) ta có hệ phương trình:
Chọn z = 3. Khi đó hệ (1) trở thành.
\(\left\{ {\begin{array}{*{20}{c}}{x - y = 0}\\{3x - 2z = 0}\end{array}} \right.\)
Vậy ta có phương trình sau cân bằng: \(2KCl{O_3}\;\mathop \to \limits^{{t^o}} \;2KCl + 3{O_2}\)
Giá trị biểu thức: \(A = 2.2 - 2 + 3.3 = 11\)
Cân bằng phương trình sau:
\(xFeC{l_2} + yC{l_2}\;\mathop \to \limits^{{t^o}} \;zFeC{l_3}\)
Giá trị biểu thức: \(A = x - 2y + z\) là:
Giá trị biểu thức: \(A = x - 2y + z\) là:
Theo định luật bảo toàn nguyên tố với Fe và Cl, ta có:
x = z hay x – z = 0
2x + 2y = 3z hay 2x + 2y – 3z = 0.
Ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x - z = 0}\\{2x + 2y - 3z = 0}\end{array}} \right.\)
Chọn z = 2. Khi đó hệ (1) trở thành
\(\left\{ {\begin{array}{*{20}{c}}{x - 2 = 0}\\{2x + 2y - 6 = 0}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2}\\{y = 1}\end{array}} \right.\)
Vậy ta có phương trình sau cân bằng: \(2FeC{l_2} + C{l_2}\;\mathop \to \limits^{{t^o}} \;2FeC{l_3}\).
Giá trị biểu thức: \(A = 2 - 2.1 + 2\) là: 2
Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177. Trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 47. Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8.
Số hạt proton trong một nguyên tử B là:
Số hạt proton trong một nguyên tử B là:
Gọi ZA, NA lần lượt là số lượng hạt p, n của nguyên tử A.
ZB, NB lần lượt là số lượng hạt p, n của nguyên tử B.
Theo đề bài:
– Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177 nên ta có:
(2ZA + NA) + (2ZB + NB) = 177 (1).
– Số hạt mang điện nhiều hơn số hạt không mang điện là 47 nên ta có:
(2ZA + 2ZB) – (NA + NB) = 47 (2).
– Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8 nên ta có:
2ZB – 2ZA = 8 hay ZB – ZA = 4 (3).
Cộng theo từng vế của (1) với (2) ta được: 4ZA + 4ZB = 224 hay ZA + ZB = 56 (4).
Từ (3) và (4) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{{Z_B} - {Z_A} = 4}\\{{Z_A} + {Z_B} = 56}\end{array}} \right.\)
Giải hệ này ta được ZA = 26, ZB = 30.
Vậy số hạt proton trong một nguyên tử B là 30.
Một đại lí bán ba mẫu máy điều hoà A, B và C, với giá bán mỗi chiếc theo từng mẫu lần lượt là 8 triệu đồng, 10 triệu đồng và 12 triệu đồng. Tháng trước, đại lí bán được 100 chiếc gồm cả ba mẫu và thu được số tiền là 980 triệu đồng. Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau. Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z.
Giá trị biểu thức \(B = 3x - y - z\) là:
Giá trị biểu thức \(B = 3x - y - z\) là:
Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Đại lí bán được 100 chiếc gồm cả ba mẫu, suy ra:
x + y + z = 100 (1).
- Số tiền thu được là 980 triệu đồng, suy ra:
8x + 10y + 12z = 980 hay 4x + 5y + 6z = 490 (2).
- Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau, suy ra
8x = 12z hay 2x –3z = 0 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{4x + 5y + 6z = 490}\\{2x - 3z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 30, y = 50, z = 20.
Vậy \(B = 3.30 - 50 - 20 = 20\)
Một đại lí bán ba mẫu máy điều hoà A, B và C, với giá bán mỗi chiếc theo từng mẫu lần lượt là 8 triệu đồng, 10 triệu đồng và 12 triệu đồng. Tháng trước, đại lí bán được 100 chiếc gồm cả ba mẫu và thu được số tiền là 980 triệu đồng. Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau. Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z.
Giá trị biểu thức \(B = 2x - 3y + 5z\) là:
Giá trị biểu thức \(B = 2x - 3y + 5z\) là:
Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Đại lí bán được 100 chiếc gồm cả ba mẫu, suy ra:
x + y + z = 100 (1).
- Số tiền thu được là 980 triệu đồng, suy ra:
8x + 10y + 12z = 980 hay 4x + 5y + 6z = 490 (2).
- Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau, suy ra
8x = 12z hay 2x –3z = 0 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{4x + 5y + 6z = 490}\\{2x - 3z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 30, y = 50, z = 20.
Vậy\(B = 2.30 - 3.50 + 5.20 = 10\)
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra.
Số tế bào con loại B lúc ban đầu là:
Số tế bào con loại B lúc ban đầu là:
Gọi số tế bào con mỗi loại A, B, C lúc ban đầu lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7.
Suy ra số tế bào con mỗi loại A, B, C được tạo ra lần lượt là:
23x, 24y và 27z hay 8x, 16y và 128z.
- Tổng số tế bào con tạo ra là 480, suy ra:
8x + 16y + 128z = 480 (1).
- Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C, suy ra:
y = x + z hay x – y + z = 0 (2).
– Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra, suy ra:
\(8x + 128z = 2.16y{\rm{ }} \Leftrightarrow 8x-32y + 128z = 0{\rm{ }} \Leftrightarrow {\rm{ }}x-4y + 16z = 0{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{8x + 16y + 127z = 480}\\{x - y + z = 0}\\{x - 4y + 16z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 8, y = 10, z = 2.
Vậy số tế bào con loại C lúc ban đầu là: 2
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra.
Số tế bào con loại B lúc ban đầu là:
Số tế bào con loại B lúc ban đầu là:
Gọi số tế bào con mỗi loại A, B, C lúc ban đầu lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7.
Suy ra số tế bào con mỗi loại A, B, C được tạo ra lần lượt là:
\(2^3x, 2^4y\) và $ 2^7z$ hay $8x, 16y$ và $128z$
- Tổng số tế bào con tạo ra là 480, suy ra:
$ 8x + 16y + 128z = 480 (1).$
- Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C, suy ra:
$y = x + z$ hay $x – y + z = 0 (2).$
– Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra, suy ra:
\(8x + 128z = 2.16y{\rm{ }} \Leftrightarrow 8x-32y + 128z = 0{\rm{ }}\\ \Leftrightarrow {\rm{ }}x-4y + 16z = 0{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{8x + 16y + 127z = 480}\\{x - y + z = 0}\\{x - 4y + 16z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 8, y = 10, z = 2.
Số tế bào con loại A lúc ban đầu là: 8
sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bảng sau.
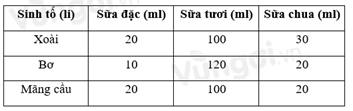
Ngày hôm qua cửa hàng đã dùng hết 2 lít sữa đặc; 12,8 lít sữa tươi và 2,9 lít sữa chua.
Số li sinh tố bơ cửa hàng bán được trong ngày hôm qua là:
Số li sinh tố bơ cửa hàng bán được trong ngày hôm qua là:
Gọi số li sinh tố mỗi loại xoài, bơ, mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Cửa hàng đã dùng hết 2 l hay 2000 ml sữa đặc, suy ra:
20x + 10y + 20z = 2000 hay 2x + y + 2z = 200 (1).
- Cửa hàng đã dùng hết 12,8 l hay 12800 ml sữa tươi, suy ra:
100x + 120y + 100z = 12800 hay 5x + 6y + 5z = 640 (2).
- Cửa hàng đã dùng hết 2,9 l hay 2900 ml sữa chua, suy ra:
30x + 20y + 20z = 2900 hay 3x + 2y + 2z = 290 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x + y + 2z = 200}\\{5x + 6y + 5z = 640}\\{3x + 2y + 2z = 290}\end{array}} \right.\)
Giải hệ này ta được x = 50, y = 40, z = 30.
Vậy số li sinh tố bơ cửa hàng bán được trong ngày hôm qua là 40.
Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bảng sau.
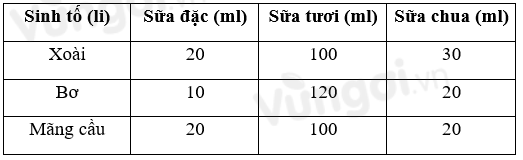
Ngày hôm qua cửa hàng đã dùng hết 2 lít sữa đặc; 12,8 lít sữa tươi và 2,9 lít sữa chua.
Số li sinh tố mãng cầu cửa hàng bán được trong ngày hôm qua là: 30
Số li sinh tố mãng cầu cửa hàng bán được trong ngày hôm qua là:
Số li sinh tố mãng cầu cửa hàng bán được trong ngày hôm qua là:
Gọi số li sinh tố mỗi loại xoài, bơ, mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là x, y, z (li)\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Cửa hàng đã dùng hết 2 l hay 2000 ml sữa đặc, suy ra:
20x + 10y + 20z = 2000 hay 2x + y + 2z = 200 (1).
- Cửa hàng đã dùng hết 12,8 l hay 12800 ml sữa tươi, suy ra:
100x + 120y + 100z = 12800 hay 5x + 6y + 5z = 640 (2).
- Cửa hàng đã dùng hết 2,9 l hay 2900 ml sữa chua, suy ra:
30x + 20y + 20z = 2900 hay 3x + 2y + 2z = 290 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x + y + 2z = 200}\\{5x + 6y + 5z = 640}\\{3x + 2y + 2z = 290}\end{array}} \right.\)
Giải hệ này ta được x = 50, y = 40, z = 30.
Vậy số li sinh tố mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là 30.
Cho mạnh điện như hình bên dưới. Biết \(U = 20\,\,V;\,\,R = 0,5\,\Omega ;\,\,{r_1} = 1\Omega ;\,\,{r_2} = 2\Omega \). Tìm cường độ dòng điện \({I_1},{I_2},\,I\) chạy qua mỗi điện trở.

D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cường độ dòng điện của đoạn mạch mắc song song là: \({I_1} + I\).
Ta có: \({I_2}\; = {I_1} + I\) hay \(I + {\rm{ }}{I_1}-{\rm{ }}{I_2}\; = 0\left( 1 \right).\)
Hiệu điện thế ở đoạn mạch mắc song song là: \(U' = {r_1}.{I_{1\;}} = R.I\) nên
\(1.{\rm{ }}{I_{1\;}} = 2.{\rm{ }}I\) hay \(2I-{I_1}\; = 0\left( 2 \right).\)
Hiệu điện thế của cả đoạn mạch là: \(U = {U_{2\;}} + U'\) nên:
\(20 = {r_2}.{\rm{ }}{I_2} + R.I\) hay \(2I + 0,5{I_2}\; = 20\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I + {I_1} - {I_2} = 0}\\{2I - {I_1} = 0}\\{2I + 0,5{I_2} = 20}\end{array}} \right.\)
Giải hệ phương trình, ta được:
\(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cho mạnh điện như hình bên dưới. Biết \(U = 20\,\,V;\,\,R = 0,5\,\Omega ;\,\,{r_1} = 1\Omega ;\,\,{r_2} = 2\Omega \). Tìm cường độ dòng điện \({I_1},{I_2},\,I\) chạy qua mỗi điện trở.

D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cường độ dòng điện của đoạn mạch mắc song song là: \({I_1} + I\).
Ta có: \({I_2}\; = {I_1} + I\) hay \(I + {\rm{ }}{I_1}-{\rm{ }}{I_2}\; = 0\left( 1 \right).\)
Hiệu điện thế ở đoạn mạch mắc song song là: \(U' = {r_1}.{I_{1\;}} = R.I\) nên
\(1.{\rm{ }}{I_{1\;}} = 2.{\rm{ }}I\) hay \(2I-{I_1}\; = 0\left( 2 \right).\)
Hiệu điện thế của cả đoạn mạch là: \(U = {U_{2\;}} + U'\) nên:
\(20 = {r_2}.{\rm{ }}{I_2} + R.I\) hay \(2I + 0,5{I_2}\; = 20\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I + {I_1} - {I_2} = 0}\\{2I - {I_1} = 0}\\{2I + 0,5{I_2} = 20}\end{array}} \right.\)
Giải hệ phương trình, ta được:
\(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cho mạch điện như hình sau. Biết U = 24 V, Ð1:12 V – 6 W, Ð2:12 V – 12 W, R = 3 Ω.

Điện trở của mỗi bóng đèn Đ1 và Đ2 là:
Điện trở của Đ1 là: R1 = \(\dfrac{{{{12}^2}}}{6}\)=24(Ω).
Điện trở của Đ2 là: R2 = \(\dfrac{{{{12}^2}}}{{12}}\)=12(Ω).

