Hệ bất phương trình bậc nhất hai ẩn
Sách kết nối tri thức với cuộc sống
Đề mẫu ĐGNL 2019
Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dữ trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Để đạt được lợi nhuận cao nhất, bác nông dân đã trồng \(x\left( {ha} \right)\) lúa và \(y\left( {ha} \right)\) khoai. Giá trị của \(x\) là:
Bước 1:
Gọi \(x,y\) (ha) lần lượt là diện tích đất cây trồng lúa và khoai \(\left( {x,y > 0} \right)\).
Tổng diện tích lúa và khoai được trồng là \(x + y\) (ha).
Tổng lượng phân bón cần dùng là \(20x + 10y\) (kg).
Tổng số ngày công cần dùng là \(10x + 30y\) (ngày).
Lợi nhuận thu được là \(S\left( {x;y} \right) = 30x + 60y\) (triệu đồng)
Từ giả thiết ta được hệ bất phương trình thể hiện miền nghiệm là:
\(\left\{ \begin{array}{l}x + y \le 6\\20x + 10y \le 100\\10x + 30y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\)
Bước 2:
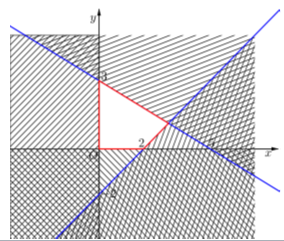
Ta biểu thị miền nghiệm của hệ bất phương trình bởi bằng đồ thị:

Miền nghiệm của hệ bất phương trình là ngũ giác \(OABCD\) vớ \(O\left( {0;0} \right),A\left( {0;4} \right),B\left( {3;3} \right),C\left( {4;2} \right),D\left( {5;0} \right)\).
Bước 3:
Khi đó \(S\left( {x;y} \right)\) đạt giá trị lớn nhất tại một trong các điểm O, A, B, C, D.
Ta có:
\(\begin{array}{l}S\left( O \right) = S\left( {0;0} \right) = 30.0 + 60.0 = 0\\S\left( A \right) = S\left( {0;4} \right) = 30.0 + 60.4 = 240\\S\left( B \right) = S\left( {3;3} \right) = 30.3 + 60.3 = 270\\S\left( C \right) = S\left( {4;2} \right) = 30.4 + 60.2 = 240\\S\left( D \right) = S\left( {5;0} \right) = 30.5 + 60.0 = 150\end{array}\)
Ta thấy \(S\left( {3;3} \right) = 270\) là giá trị lớn nhất khi \(x = y = 3\).
Vậy \(x = 3\).
Một công ty kinh chuẩn bị cho đợt khuyến mại nhằm mục đích thu hút khác hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên internet và truyền hình. Chi phí cho 1 phút quảng cáo trên internet là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Trang internet chỉ nhận phát các chương trình quảng cáo ngắn nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dì tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên internet. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên internet và truyền hình như thế nào để hiệu quả nhất?
Bước 1:
Gọi thời lượng công ty đặt quảng cáo trên internet là x (phút)\(\left( {x \ge 0} \right)\), trên truyền hình là y (phút)\(\left( {y \ge 0} \right)\).
Bước 2:
Chi phí cho việc quảng cáo là \(800000x + 4000000y\).
Vì mức chi phí tối đa là 16.000.000 đồng nên ta có bất phương trình:
\(\begin{array}{l}800000x + 4000000y \le 16000000\\ \Leftrightarrow x + 5y - 20 \le 0\end{array}\)
Do các điều kiện của internet và truyền hình nên ta có: \(x \ge 5,y \le 4\).
Hiệu quả chung của quảng cáo là \(x + 6y\).
Bước 3:
Bài toán trở thành: Xác định \(x,y\) sao cho \(M\left( {x;y} \right) = x + 6y\) đạt giá trị lớn nhất.
Với điều kiện \(\left\{ \begin{array}{l}x + 5y - 20 \le 0\\x \ge 5\\y \ge 0\\y \le 4\end{array} \right.\left( * \right)\)
Bước 4:
Xác định miền nghiệm của hệ (*):
Trong mặt phẳng tọa độ vẽ các đường thẳng \(\left( d \right):x + 5y - 20 = 0;\left( {d'} \right):x = 5;\)\(\left( {d''} \right):y = 4\).
Khi đó miền nghiệm của hệ (*) là phần mặt phẳng (tam giác) bị tô màu trên hình vẽ

Bước 5:
\(M\left( {x;y} \right) = x + 6y\) đạt giá trị lớn nhất tại một trong các điểm \(\left( {5;3} \right),\left( {5;0} \right),\left( {20;0} \right)\).
Ta có: \(M\left( {5;3} \right) = 23;M\left( {5;0} \right) = 5;\)\(M\left( {20;0} \right) = 20\).
Vậy nếu đặt thời lượng quảng cáo trên internet là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?
Thay lần lượt tọa độ các điểm vào hệ bất phương trình ta thấy chỉ có điểm $\left( {0;0} \right)$ không thỏa mãn hệ.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?
Dễ thấy \(x = - \dfrac{1}{4};y = - 1\) thỏa mãn cả hai bất phương trình nên \(\left( { - \dfrac{1}{4}; - 1} \right) \in S\), do đó A sai.
Ta sẽ biểu diễn tập nghiệm của bất phương trình trên mặt phẳng tọa độ như sau:
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x - \dfrac{3}{2}y = 1\)
\(\left( {{d_2}} \right):4x - 3y = 2\)
Thử trực tiếp ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của bất phương trình (2) vì 4.0-3.0 < 2 (đúng)
Nhưng (0;0) không phải là nghiệm của bất phương trình (1) vì \(2.0 - \dfrac{3}{2}.0 < 1\).
Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng \(\left( d \right):4x - 3y = 2.\)
Cho hệ \(\left\{ \begin{array}{l}2x + 3y < 5\,\,\,(1)\\x + \dfrac{3}{2}y < 5\,\,\,(2)\end{array} \right.\). Gọi \({S_1}\) là tập nghiệm của bất phương trình (1), \({S_2}\) là tập nghiệm của bất phương trình (2) và \(S\) là tập nghiệm của hệ thì
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x + 3y = 5\)
\(\left( {{d_2}} \right):x + \dfrac{3}{2}y = 5\)
Ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
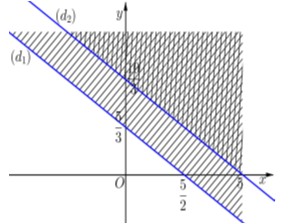
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D ?
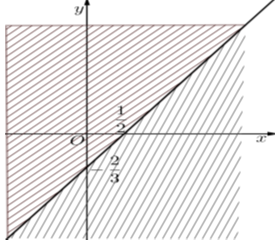
Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng \(\left( {{d_1}} \right):y = 0\) và đường thẳng \(\left( {{d_2}} \right):3x + 2y = 6.\)
Miền nghiệm gồm phần \(y\) nhận giá trị dương.
Lại có \(\left( {0\,\,;\,\,0} \right)\) thỏa mãn bất phương trình \(3x + 2y < 6.\)
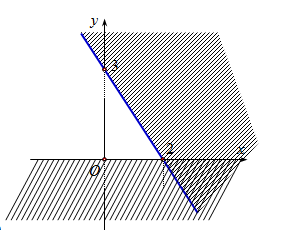
Miền tam giác \(ABC\) kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D ?
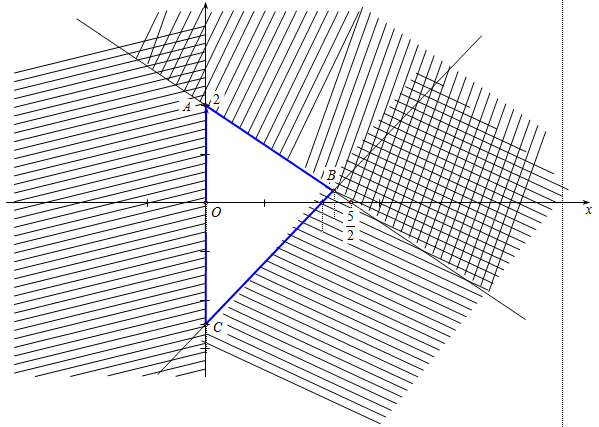
Dựa vào hình vẽ, ta thấy:
Đường thẳng \(\left( {{d_1}} \right)\) là trục tung Oy nên có phương trình x=0.
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm (0;2) và \((\dfrac{5}{2};0)\) nên có phương trình \(\frac{x}{{\frac{5}{2}}} + \frac{y}{2} = 1 \Leftrightarrow \frac{{2x}}{5} + \frac{y}{2} = 1 \Leftrightarrow 4x + 5y = 10\)
Đường thẳng \(\left( {{d_3}} \right)\) đi qua các điểm (2;0) và \((0;-\dfrac{5}{2})\) nên có phương trình \(\frac{x}{2} + \frac{y}{{ - \frac{5}{2}}} = 1 \Leftrightarrow \frac{x}{2} - \frac{{2y}}{5} = 1 \Leftrightarrow 5x - 4y = 10\)
Miền nghiệm gần phần mặt phẳng nhận giá trị \(x\) dương (kể cả bờ \(\left( {{d_1}} \right)\)).
Lại có \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của cả hai bất phương trình \(4x + 5y \le 10\) và \(5x - 4y \le 10.\)
Vậy miền tam giác ABC biểu diễn nghiệm của hệ câu C.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\3x + 5y \le 15\\x \ge 0\\y \ge 0\end{array} \right.\). Khẳng định nào sau đây là khẳng định sai ?
Trước hết, ta vẽ bốn đường thẳng:
\(\left( {{d_1}} \right):x - y = 2\)
\(\left( {{d_2}} \right):3x + 5y = 15\)
\(\left( {{d_3}} \right):x = 0\)
\(\left( {{d_4}} \right):y = 0\)
- Miền nghiệm là phần không bị gạch, kể cả biên nên A đúng.
- Đáp án B sai vì nếu \(m = 5\) ta vẽ đường thẳng \(x + y = 5\) sẽ không có giao điểm với miền nghiệm của hệ.
- Ta sẽ tìm GTLN, GTNN của biểu thức \(F\left( {x;y} \right) = x + y\) với \(\left( {x;y} \right)\) là nghiệm của hệ.
Ta có:
\(\begin{array}{l}F\left( {0;3} \right) = 0 + 3 = 3,F\left( {\dfrac{{25}}{8};\dfrac{9}{8}} \right) = \dfrac{{25}}{8} + \dfrac{9}{8} = \dfrac{{17}}{4},\\F\left( {2;0} \right) = 2 + 0 = 2,F\left( {0;0} \right) = 0 + 0 = 0\end{array}\)
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa $24$ $g$ hương liệu, $9$ lít nước và $210$ $g$ đường để pha chế nước cam và nước táo.
+ Để pha chế $1$ lít nước cam cần $30$ $g$ đường, $1$ lít nước và $1$ $g$ hương liệu;
+ Để pha chế $1$ lít nước táo cần $10$ $g$ đường, $1$ lít nước và $4$ $g$ hương liệu.
Mỗi lít nước cam nhận được $60$ điểm thưởng, mỗi lít nước táo nhận được $80$ điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Giả sử $x,{\rm{ }}y$ lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
Suy ra $30x + 10y$ là số gam đường cần dùng;
$x + y$ là số lít nước cần dùng;
$x + 4y$ là số gam hương liệu cần dùng.
Theo giả thiết ta có $\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\30x + 10y \le 210\\x + y \le 9\\x + 4y \le 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x + y \le 21\\x + y \le 9\\x + 4y \le 24\end{array} \right..$ \(\left( * \right)\)
Số điểm thưởng nhận được sẽ là $P\left( {x;y} \right) = 60x + 80y.$
Ta đi tìm giá trị nhỏ nhất của biểu thức \(P\) với \(x,{\rm{ }}y\) thỏa mãn \(\left( * \right)\).

Miền nghiệm là phần hình vẽ không tô màu ở hình trên, hay là ngũ giác \(OBCDE\) với \(O\left( {0;0} \right),B\left( {0;6} \right),C\left( {4;5} \right),D\left( {6;3} \right),E\left( {7;0} \right)\).
Biểu thức $P = 60x + 80y$ đạt GTLN tại \(\left( {x;y} \right)\) là tọa độ một trong các đỉnh của ngũ giác.
Thay lần lượt tọa độ các điểm \(O,B,C,D,E\) vào biểu thức \(P\left( {x;y} \right)\) ta được:
\(P\left( {0;0} \right) = 0;P\left( {0;6} \right) = 480;P\left( {4;5} \right) = 640;P\left( {6;3} \right) = 600;P\left( {7;0} \right) = 420\)
Giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ là.
Biểu diễn miền nghiệm của hệ bất phương trình $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ trên hệ trục tọa độ như dưới đây:
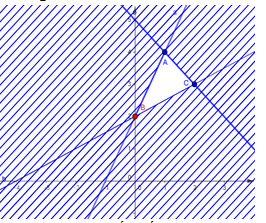
Nhận thấy biết thức $F = y - x$ chỉ đạt giá trị nhỏ nhất tại các điểm \(A,B\) hoặc \(C\).
Ta có: \(F\left( A \right) = 4 - 1 = 3;\,F\left( B \right) = 2;\,F\left( C \right) = 3 - 2 = 1\).
Vậy ${\rm{min }}F = 1$ khi $x = 2,y = 3$.
Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin \(A\) và \(B\) đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả \(A\) lẫn \(B\) và có thể tiếp nhận không quá 600 đơn vị vitamin \(A\)và không quá 500 đơn vị vitamin \(B\). Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin \(B\) không ít hơn một nửa số đơn vị vitamin \(A\) và không nhiều hơn ba lần số đơn vị vitamin \(A\). Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin \(A\) có giá 9 đồng và mỗi đơn vị vitamin \(B\) có giá 7,5 đồng.
Gọi \(x \ge 0,{\rm{ }}y \ge 0\) lần lượt là số đơn vị vitamin \(A\) và \(B\) để một người cần dùng trong một ngày.
Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị vitamin cả \(A\) lẫn \(B\) nên ta có: \(400 \le x + y \le 1000.\)
Hàng ngày, tiếp nhận không quá 600 đơn vị vitamin \(A\)và không quá 500 đơn vị vitamin \(B\)nên ta có: \(x \le 600,{\rm{ }}y \le 500.\)
Mỗi ngày một người sử dụng số đơn vị vitamin \(B\) không ít hơn một nửa số đơn vị vitamin \(A\) và không nhiều hơn ba lần số đơn vị vitamin \(A\)nên ta có: \(0,5x \le y \le 3x.\)
Số tiền cần dùng mỗi ngày là: \(T\left( {x,y} \right) = 9x + 7,5y.\)
Bài toán trở thành: Tìm \(x \ge 0,{\rm{ }}y \ge 0\) thỏa mãn hệ \(\left\{ \begin{array}{l}0 \le x \le 600,0 \le y \le 500\\400 \le x + y \le 1000\\0,5x \le y \le 3x\end{array} \right.\) để \(T\left( {x,y} \right) = 9x + 7,5y\) đạt giá trị nhỏ nhất.
Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ :

Miền nghiệm là lục giác \(ABCDEF\) với
\(\begin{array}{l}A\left( {\dfrac{{500}}{3};500} \right),B\left( {100;300} \right),C\left( {\dfrac{{800}}{3};\dfrac{{400}}{3}} \right)\\D\left( {600;300} \right),E\left( {600;400} \right),F\left( {500;500} \right)\end{array}\)
Thay tọa độ các điểm \(A,B,C,D,E,F\) vào biểu thức \(T\left( {x,y} \right) = 9x + 7,5y\) và tìm GTNN của nó ta được:
\(\begin{array}{l}T\left( {\dfrac{{500}}{3};500} \right) = 5250,T\left( {100;300} \right) = 3150,T\left( {\dfrac{{800}}{3};\dfrac{{400}}{3}} \right) = 3400\\T\left( {600;300} \right) = 7650,T\left( {600;400} \right) = 8400,T\left( {500;500} \right) = 8250\end{array}\)
Vậy \(\min T\left( {x;y} \right) = 3150\) khi \(x = 100;y = 300\)
Miền biểu diễn nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y \ge - 2\\x \ge 2\\2x + y \le 8\end{array} \right.\) có diện tích bằng bao nhiêu?
Dễ thấy miền nghiệm của hệ bất phương trình là tam giác vuông tại B với 3 đỉnh là \(A\left( {2;4} \right),B\left( {2; - 2} \right),C\left( {5; - 2} \right)\)
\(\begin{array}{l} \Rightarrow AB = 6,\,\,BC = 3\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.6.3 = 9.\end{array}\)
Thay tọa độ điểm \(M\left( {1;\;0} \right)\) vào hệ BPT ta có: \(\left\{ \begin{array}{l}2.1 - 0 = 2 \le 3\\10.1 + 5.0 = 10 > 8\end{array} \right.\)
Vậy điểm \({M_0}\left( {1;0} \right)\) thuộc miền nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x - y \le 3\\10x + 5y > 8\end{array} \right.\)
Một công ty Y cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có 2 loại xe, trong đó có 10 xe loại \(A\) và 9 xe loại \(B\). Một chiếc xe loại \(A\) cho thuê với giá 4 triệu, một chiếc xe loại \(B\) cho thuê với giá 3 triệu. Biết rằng mỗi xe loại \(A\) có thể chở 20 người và 0,6 tấn hàng; mỗi xe loại \(B\) có thể chở tối đa 10 người và 1,5 tấn Công ty X cần thuê bao nhiêu xe mỗi loại để chi phí bỏ ra ít nhất?
5 xe loại \({\rm{A}}\) và 4 xe loại \({\rm{B}}\)
5 xe loại \({\rm{A}}\) và 4 xe loại \({\rm{B}}\)
5 xe loại \({\rm{A}}\) và 4 xe loại \({\rm{B}}\)
Bước 1: Gọi x và y lần lượt là số loại xe A và B cần thuê. Biểu diễn các đại lượng khác theo x và y
Gọi x và y lần lượt là số loại xe A và B cần thuê. Khi đó số tiền cần bỏ ra để thuê xe là \(f(x;y) = 4x + 3y\) (triệu).
Ta có \(x\) xe loại \(A\) sẽ chở được 20x người và 0,3x tấn hàng; \(y\) xe loại \(B\) sẽ chở được 10y người và 1,5y tấn hàng.
Bước 2: Lập hệ bất phương trình
Ta có hệ bất phương trình sau
\(\left\{ {\begin{array}{*{20}{l}}{20x + 10y \ge 140}\\{0,6x + 1,5y \ge 9}\\{0 \le x \le 10}\\{0 \le y \le 9}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2x + y \ge 14}\\{2x + 5y \ge 30}\\{0 \le x \le 10}\\{0 \le y \le 9}\end{array}(*)} \right.\)
Bước 3: Biểu diễn tập nghiệm.
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số \(f(x;y)\) trên miền nghiệm của hệ \((*)\). Miền nghiệm của hệ \((*)\) là tứ giác ABCD (kể cả biên).

Bước 4: Tìm x và y.
Hàm số \(f(x;y) = 4x + 3y\) sẽ đạt giá trị nhỏ nhất trên miền nghiệm của hệ bất phương trình \((*)\) khi \((x;y)\) là tọa độ của một trong các đỉnh \(A(5;4)\), \(B(10;2),C(10;9);D\left( {\dfrac{5}{2};9} \right)\).
Ta có \(f(5;4) = 32;f(10;2) = 46;\)
\(f(10;9) = 67;f\left( {\dfrac{5}{2};9} \right) = 37.\)
Suy ra \(f(x;y)\) nhỏ nhất khi \((x;y) = (5;4)\). Như vậy để chi phí vận chuyển thấp nhất cần thuê 5 xe loại \({\rm{A}}\) và 4 xe loại \({\rm{B}}\).

