Trong tam giác \(ABC\) có:
Ta có: ${a^2} = {b^2} + {c^2} - 2bc\cos A$
Trong tam giác\(ABC\) có
Ta có: \(\dfrac{a}{{\sin \,A}} = \dfrac{b}{{\sin \,B}} = \dfrac{c}{{\sin \,C}} = 2R \Rightarrow a = 2R\sin A.\)
Trong tam giác $ABC$ ta có:
Ta có: \(\dfrac{a}{{\sin \,A}} = \dfrac{b}{{\sin \,B}} = \dfrac{c}{{\sin \,C}} = 2R \Rightarrow a\sin B = b\sin A.\)
Trong tam giác $ABC$, ta có.
Ta có \(\dfrac{1}{2}a.{h_a} = \dfrac{{abc}}{{4R}}\). Suy ra \({h_a} = \dfrac{{bc}}{{2R}}.\) hay \(bc = 2R.{h_a}\).
Trong tam giác $ABC$, tìm hệ thức sai.
+ ) \(\dfrac{1}{2}a.{h_a} = \dfrac{1}{2}ab.\sin C = \dfrac{1}{2}ac.\sin B\)
Suy ra \({h_a} = b.\sin C = c.\sin B\). Suy ra mệnh đề đáp án A và B đúng.
+ ) \(\dfrac{1}{2}c.{h_c} = \dfrac{1}{2}ab.\sin C\). Suy ra \(c.{h_c} = ab.\sin C\). Suy ra mệnh đề đáp án D đúng.
Cho tam giác $ABC$ có \(\widehat B = {60^0},\widehat C = {45^0}\) và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?
\(\dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} \Rightarrow b = \dfrac{c}{{\sin C}}.\sin B = \dfrac{5}{{\sin {{45}^0}}}.\sin {60^0} = \dfrac{{5\sqrt 6 }}{2}.\)
Cho tam giác $ABC$ có $b = 10,c = 16$ và góc \(\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài của cạnh $BC$?
$\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\ = {10^2} + {16^2} - 2.10.16.\cos {60^0}\\ = {\rm{ }}196\end{array}$ .
Suy ra \(BC = a = \sqrt {196} = 14\).
Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).
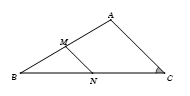
Bước 1: Tính \(AC\)
Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\).
\( \Rightarrow MN\) là đường trung bình của \(\Delta ABC\).
\( \Rightarrow MN = \dfrac{1}{2}AC\). Mà \(MN = 3\), suy ra \(AC = 6\).
Bước 2: Sử dụng định lý cô sin cho tam giác \(ABC\)
Theo định lí hàm cosin, ta có
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\\ \Leftrightarrow {9^2} = {6^2} + B{C^2} - 2.6.BC.\cos 60^\circ \\ \Rightarrow BC = 3 + 3\sqrt 6 \end{array}\)
Tam giác $ABC$ có ba cạnh là $5,12,13$. Khi đó, diện tích tam giác là:
+ Ta có \(p = \dfrac{{a + b + c}}{2} = \dfrac{{5 + 12 + 13}}{2} = 15\)
+ \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15.10.3.2} = \sqrt {900} = 30\)
Tam giác $ABC$ có $BC = a,CA = b,AB = c$ và có diện tích $S$ . Nếu tăng cạnh $BC$ lên $2$ lần đồng thời tăng cạnh $CA$ lên $3$ lần và giữ nguyên độ lớn của góc $C$ thì khi đó diện tích tam giác mới được tạo nên bằng:
+ Có \(S = \dfrac{1}{2}BC.CA.\sin C\)
+ Gọi $S'$ là diện tích tam giác khi tăng cạnh $BC$ lên $2$ lần đồng thời tăng cạnh $CA$ lên $3$ lần và giữ nguyên độ lớn của góc $C$ , ta có: \(S' = \dfrac{1}{2}.2BC.3CA.\sin C = 6S\)
Tam giác $ABC$ có $BC = 10$ và \(\widehat A = {30^0}\). Khi đó, bán kính đường tròn ngoại tiếp tam giác $ABC$ là:
Từ \(\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{BC}}{{2\sin A}} = \dfrac{{10}}{{2\sin {{30}^0}}} = 10\)
Tam giác vuông cân tại $A$ có $AB = 2a$. Đường trung tuyến $BM$ có độ dài là:
+ Ta có $AB = AC = 2a$ .
+ Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {4{a^2} + 4{a^2}} = 2\sqrt 2 a\)
+ \(MB_{}^2 = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{8{a^2} + 4{a^2}}}{2} - \dfrac{{4{a^2}}}{4} = 5{a^2} \Rightarrow MB = a\sqrt 5 \)
Nếu tam giác $ABC$ có \({a^2} < {b^2} + {c^2}\) thì
Ta có \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Theo giả thiết \({a^2} < {b^2} + {c^2} \Rightarrow \cos A > 0\).
Vậy góc $A$ nhọn.
Cho tam giác $ABC$ có $AB = 8cm,AC = 18cm$ và có diện tích bằng \(64c{m^2}\). Giá trị $\sin \widehat A$ là:
Ta có \(S = \dfrac{1}{2}AB.AC.\sin A \Rightarrow \sin A = \dfrac{{2S}}{{AB.AC}} = \dfrac{{2.64}}{{8.18}} = \)\(\dfrac{8}{9}\)
Cho tam giác $ABC$ có $AB = 4cm,BC = 7cm,CA = 9cm$. Giá trị $\cos A$ là:
Ta có \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \dfrac{{{9^2} + {4^2} - {7^2}}}{{2.9.4}} = \dfrac{2}{3}\)
Tam giác $ABC$ có ba cạnh là $6,8,10$ . Khi đó, bán kính đường tròn nội tiếp tam giác $ABC$ là:
+ Ta có \(p = \dfrac{{6 + 8 + 10}}{2} = 12\)
+ \(S = \sqrt {p(p - a)(p - b)(p - c)} \)=\(\sqrt {12.6.4.2} = 24\)
+ \(r = \dfrac{S}{p} = \dfrac{{24}}{{12}} = 2\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc \(\widehat {ABC} = \alpha \) và \(\widehat {ACB} = \beta \) . Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).
+ Có \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{13}^2} - {5^2}} = 12\)
+ \(\dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} \Rightarrow \dfrac{{\sin C}}{{\sin B}} = \dfrac{c}{b} = \dfrac{5}{{12}} < 1\) (*)
+ Tam giác $ABC$ vuông tại $A$ , suy ra $B$ và $C$ là góc nhọn. Do đó \(\sin B > 0\) và \(\sin C > 0\).
Từ (*) suy ra \(\sin C < \sin B\) . Suy ra $C < B$ hay \(\beta < \alpha \).
Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Độ dài lớn nhất của đoạn \(OB\) bằng:
Bước 1: Sử dụng định lý hàm số sin cho tam giác \(OAB\) tìm OB
Theo định lí hàm sin, ta có:
\(\dfrac{{OB}}{{\sin \widehat {OAB}}} = \dfrac{{AB}}{{\sin \widehat {AOB}}}\)\( \Leftrightarrow OB = \dfrac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB}\) \( = \dfrac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\)
Bước 2: Đánh giá GTLN của \(OB\).
Do đó, độ dài \(OB\) lớn nhất khi và chỉ khi \(\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \).
Khi đó \(OB = 2\).
Tam giác \(ABC\) vuông tại \(A\), có \(AB = c,\;AC = b\). Gọi \({\ell _a}\) là độ dài đoạn phân giác trong góc \(\widehat {BAC}\). Tính \({\ell _a}\) theo \(b\) và \(c\).
Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{b^2} + {c^2}} \).
Do \(AD\) là phân giác trong của \(\widehat {BAC}\)
\( \Rightarrow BD = \dfrac{{AB}}{{AC}}.DC\)\( = \dfrac{c}{b}.DC = \dfrac{c}{{b + c}}.BC = \dfrac{{c\sqrt {{b^2} + {c^2}} }}{{b + c}}\).
Theo định lí hàm cosin, ta có
\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {ABD}\)\( \Leftrightarrow \dfrac{{{c^2}\left( {{b^2} + {c^2}} \right)}}{{{{\left( {b + c} \right)}^2}}} = {c^2} + A{D^2} - 2c.AD.\cos 45^\circ \)
\( \Rightarrow A{D^2} - c\sqrt 2 .AD + \left( {{c^2} - \dfrac{{{c^2}\left( {{b^2} + {c^2}} \right)}}{{{{\left( {b + c} \right)}^2}}}} \right) = 0\)\( \Leftrightarrow A{D^2} - c\sqrt 2 .AD + \dfrac{{2b{c^3}}}{{{{\left( {b + c} \right)}^2}}} = 0\)
\( \Rightarrow AD = \dfrac{{\sqrt 2 bc}}{{b + c}}\) hay \({\ell _a} = \dfrac{{\sqrt 2 bc}}{{b + c}}\).
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
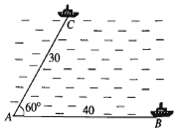
Sau \(2\) giờ tàu \(B\) đi được \(40\) hải lí, tàu \(C\) đi được \(30\) hải lí. Vậy tam giác \(ABC\) có \(AB = 40,\,\,\,AC = 30\) và \(\widehat A = {60^0}.\)
Áp dụng định lí côsin vào tam giác \(ABC,\) ta có
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)\( = {30^2} + {40^2} - 2.30.40.\cos {60^0}\)\( = 900 + 1600 - 1200 = 1300\)
Vậy \(BC = \sqrt {1300} \approx 36\) (hải lí).
Sau \(2\) giờ, hai tàu cách nhau khoảng \(36\) hải lí.

