Sự thống nhất giữa ba đường conic

Đường conic có phương trình: \(\dfrac{{{x^2}}}{{100}} + \dfrac{{{y^2}}}{{64}} = 1\) là đường elip.

Chọn hệ trục toạ độ sao cho Mặt Trời trùng với tiêu điểm \({F_1}\) của elip.

Khi đó elip có phương trình là

\(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\;\left( {a > b > 0} \right).\)

Theo đề bài, ta có: elip này có bán trục lớn \(a \approx 5,{906.10^6}\;km\) và tâm sai \(e \approx 0,249\)

Giả sử Sao Diêm Vương có toạ độ là \(M\left( {x;{\rm{ }}y} \right).\)

Khi đó khoảng cách giữa Sao Diêm Vương và Mặt Trời là: \(M{F_1}\; = a + \;ex.\)

Vì \(x \ge -a\) nên \(M{F_1}\; \ge a-ea \approx 5,{906.10^6}-0,249.5,{906.10^6}\; = 4\,435\,406{\rm{ }}\left( {km} \right).\)

Vậy khoảng cách nhỏ nhất giữa Sao Diêm Vương và Mặt Trời xấp xỉ \(4\,435\,406{\rm{ }}km.\)

Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.

Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).

Khi đó:

\(M{K^2}-M{O^2}\; = 1\)

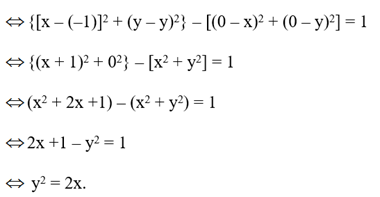
Vậy tập hợp các điểm M là parabol có phương trình \({y^2}\; = 2x.\)

Gọi M, N lần lượt là trung điểm của AB, BC.

Gọi phương trình chính tắc của elip cần tìm là \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\;\left( {a > b > 0} \right).\)

Vì ABCD là hình chữ nhật cơ sở của elip nên M, N là hai đỉnh của elip.

Lại có: \(M\left( {0;{\rm{ }}3} \right)\; \Rightarrow \;b = 3,{\rm{ }}N\left( {4;{\rm{ }}0} \right) \Rightarrow \;a = 4.\)

Vậy phương trình chính tắc của elip cần tìm là: \(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\).

Gọi phương trình chính tắc của parabol quỹ đạo là \({y^2}\; = 2px\left( {p > 0} \right).\)

Nhìn hình vẽ ta thấy: \(OF = 148 + 6371 = 6519{\rm{ }}\left( {km} \right)\)

\( \Rightarrow \;\dfrac{p}{2}\; = 6519 \Rightarrow p = 13038\)

⇒ phương trình chính tắc của parabol quỹ đạo là \({y^2}\; = 26\,076x.\)

Gọi M(x; y) là điểm bất kì thuộc conic.

Khi đó, ta có: \(\dfrac{{MF}}{{d\left( {M;\Delta } \right)}} = e\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt {{{\left( {1 - x} \right)}^2} + {{\left( {0 - y} \right)}^2}} }}{{\left| {x + 1} \right|}} = 1\\ \Leftrightarrow \sqrt {{{\left( {1 - x} \right)}^2} + {{\left( {0 - y} \right)}^2}} = \left| {x + 1} \right|\\ \Leftrightarrow {\left( {1 - x} \right)^2} + {\left( {0 - y} \right)^2} = {\left| {x + 1} \right|^2}\\ \Leftrightarrow \left( {1 - 2x + {x^2}} \right) + {y^2} = {x^2} + 2x + 1\\ \Leftrightarrow {y^2} = 4x\end{array}\)

Vậy phương trình của conic đã cho là \({y^2}\; = 4x.\)

Vì quỹ đạo của Sao Hoả có tâm sai nhỏ hơn 1 nên là đường elip.

Elip là đường conic có tâm sai e < 1

Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F₁ của elip.

Khi đó elip có phương trình là

\(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\;\left( {a > b > 0} \right).\)

Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm

Mà bán kính của Trái Đất xấp xỉ 4000 dặm

=> Vệ tinh cách tâm Trái Đất gần nhất là 583 + 4000 = 4583 dặm và xa nhất là 1342 + 4000 = 5342 dặm.

Giả sử vệ tinh có toạ độ là M(x; y).

Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là: \(M{F_1}\; = a + \;\dfrac{c}{a}x\)

Vì \(-a \le x \le a\) nên \(a-c{\rm{ }} \le M{F_1}\; \le a + c.\)

Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là a – c và a + c.

Vậy tâm sai của quỹ đạo này xấp xỉ 0,076.

Ta có: $2p = 2$

\( \Rightarrow p = 1 \Rightarrow \dfrac{p}{2} = \dfrac{1}{2}\)

Vậy tiêu điểm của parabol là \(F\left( {\dfrac{1}{2};0} \right).\)