Điểm nào sau đây thuộc đồ thị hàm số $y = 2\left| {x-1} \right| + 3\left| x \right| - 2$?
Đặt \(y = f\left( x \right) = 2\left| {x-1} \right| + 3\left| x \right| - 2\).
Ta có: \(f\left( 2 \right) = 2\left| {2-1} \right| + 3\left| 2 \right| - 2 = 6\) nên \(\left( {2;6} \right)\) thuộc đồ thị hàm số.
Cho hàm số $y = \left\{ \begin{array}{l}\dfrac{2}{{x - 1}}{\rm{ }},{\rm{ }}x \in \left( { - \infty ;0} \right)\\\sqrt {x + 1} {\rm{ }},{\rm{ }}x \in \left[ {0;2} \right]\\{x^2} - 1{\rm{ }},{\rm{ }}x \in \left( {2;5} \right]\end{array} \right.$. Tính \(f\left( 4 \right)\), ta được kết quả:
Ta thấy \(x = 4 \in \left( {2;5} \right] \Rightarrow f\left( 4 \right) = {4^2} - 1 = 15\).
Tập xác định của hàm số $y = \dfrac{{x - 1}}{{{x^2} - x + 3}}$ là
${x^2} - x + 3 = {x^2} - 2.\dfrac{1}{2}.x + \dfrac{1}{4} + \dfrac{{11}}{4} = {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{{11}}{4} > 0,\forall x \in R$
Vậy tập xác định của hàm số là \(R\).
Tập xác định của hàm số $y = \left\{ \begin{array}{l}\sqrt {3 - x} ,x \in \left( { - \infty ;0} \right)\\\sqrt {\dfrac{1}{x}} ,x \in \left( {0; + \infty } \right)\end{array} \right.$ là:
- Hàm số \(y = \sqrt {3 - x} \) luôn xác định trên $\left( { - \infty ;0} \right)$.
- Hàm số \(y = \sqrt {\dfrac{1}{x}} \) xác định trên \(\left( {0; + \infty } \right)\).
- Điểm \(x = 0\) không nằm trong tập xác định nào, do đó hàm số không xác định tại \(x = 0\).
Vậy tập xác định của hàm số là \(D = R\backslash \left\{ 0 \right\}\).
Hàm số $y = \dfrac{{x + 1}}{{x - 2m + 1}}$ xác định trên $\left[ {0;1} \right)$ khi:
Hàm số $y = \dfrac{{x + 1}}{{x - 2m + 1}}$ xác định trên $\left[ {0;1} \right)$ nếu:
\(x - 2m + 1 \ne 0,\forall x \in \left[ {0;1} \right) \Leftrightarrow x \ne 2m - 1,\forall x \in \left[ {0;1} \right)\) \(\Leftrightarrow 2m - 1 \notin [0;1) \Leftrightarrow \left[ \begin{array}{l}2m - 1 < 0\\2m - 1 \ge 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < \dfrac{1}{2}\\m \ge 1\end{array} \right.\)
Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ cùng đồng biến trên khoảng $\left( {a;b} \right)$. Có thể kết luận gì về chiều biến thiên của hàm số $y = f\left( x \right) + g\left( x \right)$ trên khoảng $\left( {a;b} \right)$?
Vì $f\left( x \right)$ và $g\left( x \right)$ cùng đồng biến trên khoảng $\left( {a;b} \right)$ nên với \({x_1},{x_2} \in \left( {a;b} \right)\) mà \({x_1} < {x_2}\) thì:
\(\left\{ \begin{array}{l}f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\\g\left( {{x_1}} \right) < g\left( {{x_2}} \right)\end{array} \right. \Rightarrow f\left( {{x_1}} \right) + g\left( {{x_1}} \right) < f\left( {{x_2}} \right) + g\left( {{x_2}} \right)\)
Do đó \(y = f\left( x \right) + g\left( x \right)\) cũng đồng biến trên \(\left( {a;b} \right)\).
Chọn A.
Trong các hàm số sau, hàm số nào tăng trên khoảng $\left( { - 1;0} \right)$?
Lấy \( - 1 < {x_1} < {x_2} < 0\) thì \({x_2} - {x_1} > 0\) ta có:
\(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{{x_2} - {x_1}}}{{{x_2} - {x_1}}} = 1 > 0,\forall {x_1},{x_2} \in \left( { - 1;0} \right)\) nên đáp án A đúng.
\(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{\dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_1}}}}}{{{x_2} - {x_1}}} = \dfrac{{{x_1} - {x_2}}}{{{x_1}{x_2}\left( {{x_2} - {x_1}} \right)}} = - \dfrac{1}{{{x_1}{x_2}}} < 0,\forall {x_1},{x_2} \in \left( { - 1;0} \right)\) nên B sai.
\(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{\left| {{x_2}} \right| - \left| {{x_1}} \right|}}{{{x_2} - {x_1}}} = \dfrac{{ - {x_2} + {x_1}}}{{{x_2} - {x_1}}} = - 1 < 0,\forall {x_1},{x_2} \in \left( { - 1;0} \right)\) nên C sai.
\(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{x_2^2 - x_1^2}}{{{x_2} - {x_1}}} = {x_2} + {x_1} < 0,\forall {x_1},{x_2} \in \left( { - 1;0} \right)\) nên D sai.
Trong các hàm số sau đây: $y = \left| x \right|$, $y = {x^2} + 4x$, $y = - {x^4} + 2{x^2}$ có bao nhiêu hàm số chẵn?
Ta thấy các hàm số đều có TXĐ là \(D = R \Rightarrow - x \in R\).
\(f\left( { - x} \right) = \left| { - x} \right| = \left| x \right| = f\left( x \right)\) nên hàm số \(y = \left| x \right|\) là hàm số chẵn.
\(f\left( { - x} \right) = {\left( { - x} \right)^2} + 4\left( { - x} \right) = {x^2} - 4x \ne {x^2} + 4x = f\left( x \right)\) nên hàm số \(y = {x^2} + 4x\) không chẵn.
$f\left( { - x} \right) = - {\left( { - x} \right)^4} + 2{\left( { - x} \right)^2} = - {x^4} + 2{x^2} = f\left( x \right)$ nên hàm số \(y = - {x^4} + 2{x^2}\) là hàm số chẵn.
Cho hàm số: $y = f\left( x \right) = \left| {2x - 3} \right|.$ Tìm \(x\) để$f\left( x \right) = 3.$
Ta có: $f\left( x \right) = \left| {2x - 3} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 3\\2x - 3 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 0\end{array} \right.$
Vậy \(x = 3\) hoặc \(x = 0\).
Câu nào sau đây đúng?
+) Hàm số $y = {a^2}x + b$ đồng biến khi \({a^2} > 0 \Leftrightarrow a \ne 0\) nên A, B và D sai.
+) Hàm số $y = - {a^2}x + b$ nghịch biến khi \( - {a^2} < 0 \Leftrightarrow a \ne 0\) nên C đúng.
Xét sự biến thiên của hàm số $y = \dfrac{1}{{{x^2}}}$. Mệnh đề nào sau đây đúng?
Ta có:
\(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{\dfrac{1}{{x_2^2}} - \dfrac{1}{{x_1^2}}}}{{{x_2} - {x_1}}} = \dfrac{{x_1^2 - x_2^2}}{{x_1^2.x_2^2\left( {{x_2} - {x_1}} \right)}} = - \dfrac{{{x_1} + {x_2}}}{{x_1^2.x_2^2}}\)
+) Nếu \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) thì \(T > 0\) nên hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
+) Nếu \({x_1},{x_2} \in \left( {0; + \infty } \right)\) thì \(T < 0\) nên hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\) và nghịch biến trên \(\left( {0; + \infty } \right)\).
Xét sự biến thiên của hàm số $y = \dfrac{x}{{x - 1}}$. Chọn khẳng định đúng.
Hàm số xác định trên \(R\backslash \left\{ 1 \right\} = \left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\).
Ta có: \(T = \dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{{\dfrac{{{x_2}}}{{{x_2} - 1}} - \dfrac{{{x_1}}}{{{x_1} - 1}}}}{{{x_2} - {x_1}}} = \dfrac{{{x_1} - {x_2}}}{{\left( {{x_2} - 1} \right)\left( {{x_1} - 1} \right)\left( {{x_2} - {x_1}} \right)}} = - \dfrac{1}{{\left( {{x_2} - 1} \right)\left( {{x_1} - 1} \right)}}\)
+) Nếu \({x_1},{x_2} \in \left( {1; + \infty } \right)\) thì \({x_1} - 1 > 0;{x_2} - 1 > 0 \Rightarrow T < 0\) nên hàm số nghịch biến trên \(\left( {1; + \infty } \right)\).
+) Nếu \({x_1},{x_2} \in \left( { - \infty ;1} \right)\) thì \({x_1} - 1 < 0;{x_2} - 1 < 0 \Rightarrow T < 0\) nên hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\).
Vậy hàm số nghịch biến trên từng khoảng xác định.
Cho hàm số:$f(x) = \left\{ \begin{array}{l}\dfrac{x}{{x + 1}},{\rm{ }}x \ge 0\\\dfrac{1}{{x - 1}},{\rm{ }}x < 0\end{array} \right.$. Giá trị $f\left( 0 \right),f\left( 2 \right),f\left( { - 2} \right)$ là
Ta thấy:
\(x = 0 \ge 0\) nên \(f\left( 0 \right) = \dfrac{0}{{0 + 1}} = 0\).
\(x = 2 \ge 0\) nên \(f\left( 2 \right) = \dfrac{2}{{2 + 1}} = \dfrac{2}{3}\).
\(x = - 2 < 0 \Rightarrow f\left( { - 2} \right) = \dfrac{1}{{ - 2 - 1}} = - \dfrac{1}{3}\).
Hàm số $y = \sqrt {\dfrac{{{x^3}}}{{\left| x \right| - 2}}} $ có tập xác định là:
Hàm số $y = \sqrt {\dfrac{{{x^3}}}{{\left| x \right| - 2}}} $ xác định nếu \(\dfrac{{{x^3}}}{{\left| x \right| - 2}} \ge 0\).
Ta có: \(\left| x \right| - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right. ; x^3=0 \Leftrightarrow x=0\)
Xét dấu biểu thức \(\dfrac{{{x^3}}}{{\left| x \right| - 2}}\) ta có:
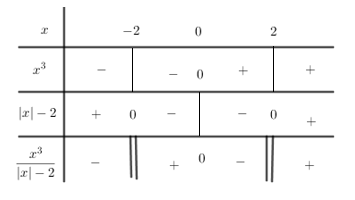
Khi đó tập xác định của hàm số là $\left( { - 2;0} \right] \cup \left( {2; + \infty } \right)$.
Cho hàm số \(y = {x^3} - 3{x^2} + 1\). Tịnh tiến đồ thị hàm số lên trên \(3\) đơn vị rồi qua phải \(2\) đơn vị ta được đồ thị hàm số không đi qua điểm nào dưới đây?
Tịnh tiến đồ thị hàm số lên trên \(3\) đơn vị rồi qua phải \(2\) đơn vị ta được đồ thị hàm số:
\(y = {\left( {x - 2} \right)^3} - 3{\left( {x - 2} \right)^2} + 1 + 3\) hay \(y = {\left( {x - 2} \right)^3} - 3{\left( {x - 2} \right)^2} + 4\).
Với \(x = 4\) thì \(y = 0\) nên A đúng.
Với \(x = 0\) thì \(y = -16\) nên B sai.
Với \(x = 2\) thì \(y = 4\) nên C đúng.
Với \(x = 3\) thì \(y = 2\) nên D đúng.
Cho hàm số \(y = m{x^2} - 2\left( {m - 1} \right)x + 1\left( {m \ne 0} \right)\) có đồ thị \(\left( {{C_m}} \right)\). Tịnh tiến \(\left( {{C_m}} \right)\) qua trái \(1\) đơn vị ta được đồ thị hàm số \(\left( {{C_m}'} \right)\). Giá trị của \(m\) để giao điểm của \(\left( {{C_m}} \right)\) và \(\left( {{C_m}'} \right)\) có hoành độ \(x = \dfrac{1}{4}\) thỏa mãn điều kiện nào dưới đây?
Phương trình \(\left( {{C_m}'} \right)\): \(y = m{\left( {x + 1} \right)^2} - 2\left( {m - 1} \right)\left( {x + 1} \right) + 1\)
Phương trình hoành độ giao điểm:
\(\begin{array}{l}m{x^2} - 2\left( {m - 1} \right)x + 1 = m{\left( {x + 1} \right)^2} - 2\left( {m - 1} \right)\left( {x + 1} \right) + 1\\ \Leftrightarrow 2mx + m - 2\left( {m - 1} \right) = 0 \Leftrightarrow 2mx - m + 2 = 0 \Leftrightarrow x = \dfrac{{m - 2}}{{2m}}\end{array}\)
Giao điểm có hoành độ \(x = \dfrac{1}{4}\) nên \(\dfrac{{m - 2}}{{2m}} = \dfrac{1}{4} \Leftrightarrow m = 4\)
Đối chiếu các đáp án ta thấy \(1 < m < 5\).
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 3;3} \right]\) để hàm số \(f\left( x \right) = \left( {m + 1} \right)x + m - 2\) đồng biến trên \(\mathbb{R}.\)
Tập xác định \({\rm{D}} = \mathbb{R}.\)
Hàm số đã cho đồng biến trên \(\mathbb{R}\) \( \Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1\).
Mà \(m \in \mathbb{Z}\) và \(m \in \left[ { - 3;3} \right]\) nên \(m \in \left\{ {0;1;2;3} \right\}\).
Tìm điều kiện của tham số để hàm số \(f\left( x \right) = a{x^2} + bx + c\) là hàm số chẵn.
Tập xác định \({\rm{D}} = \mathbb{R}\) nên \(\forall x \in {\rm{D}} \Rightarrow - x \in {\rm{D}}{\rm{.}}\)
Để \(f\left( x \right)\) là hàm số chẵn \( \Leftrightarrow f\left( { - x} \right) = f\left( x \right),{\rm{ }}\forall x \in {\rm{D}}\)
\( \Leftrightarrow a{\left( { - x} \right)^2} + b\left( { - x} \right) + c = a{x^2} + bx + c,{\rm{ }}\forall x \in \mathbb{R}\)
\( \Leftrightarrow 2bx = 0,\forall x \in \mathbb{R} \Leftrightarrow b = 0\).
Tìm tập xác định của hàm số \(y = \sqrt {x + 5} \).
Ta có: \(y = \sqrt {x + 5} \) xác định khi và chỉ khi \(x + 5 \ge 0 \Leftrightarrow x \ge - 5\).
\( \Rightarrow \) TXĐ: \(D = \left[ { - 5; + \infty } \right)\)
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 100;100} \right]\) để hàm số \(y = \dfrac{{2x + 2}}{{{x^2} - 3x + 2m - 1}}\) có tập xác định là \(\mathbb{R}?\)
Để hàm số có tập xác định là \(\mathbb{R}\) thì điều kiện xác định \({x^2} - 3x + 2m - 1 \ne 0\,\,\,\forall x\)\( \Leftrightarrow {x^2} - 3x + 2m - 1 = 0\) vô nghiệm \( \Leftrightarrow \Delta < 0\,\,\)
\(\begin{array}{l} \Leftrightarrow 9 - 4\left( {2m - 1} \right) < 0\\ \Leftrightarrow 9 - 8m + 4 < 0\\ \Leftrightarrow 13 - 8m < 0 \Leftrightarrow m > \dfrac{{13}}{8}\end{array}\)
Lại có: \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left[ { - 100;100} \right]\end{array} \right. \)\(\Rightarrow m \in \left\{ {2;\,\,3;\,\,4;...;\,\,100} \right\}\)\( \Rightarrow \) có 100-2+1=99 giá trị \(m\) thỏa mãn.
