Hypebol

$\left( H \right)\,\,:\,\dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{9} = 1 \Rightarrow a = 4,\,\,b = 3$

Tọa độ các đỉnh của $(H)$ là: ${A_1}\left( { - 4;0} \right);\,\,{A_2}\left( {4;0} \right);\,\,{B_1}\left( {0; - 3} \right);\,\,{B_2}\left( {0;3} \right)$

$(H):\,4{x^2} - {y^2} = 4 \Leftrightarrow \dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{4} = 1 $ $\Rightarrow a = 1;b = 2$

Độ dài trục thực: ${A_1}{A_2} = 2a = 2.1 = 2$

Độ dài trục ảo: ${B_1}{B_2} = 2b = 2.2 = 4$

$(H):\,\,25{x^2} - 16{y^2} = 400 \Leftrightarrow \dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{{25}} = 1 \Rightarrow a = 4,\,\,b = 5$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {c^2} = {4^2} + {5^2} = 41 \Rightarrow c = \sqrt {41} $

$ \Rightarrow $ Tiêu cự ${F_1}{F_2} = 2c = 2\sqrt {41} $.

$(H):\,\,{x^2} - {y^2} = 1 \Rightarrow a = b = 1$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {c^2} = {1^2} + {1^2} = 2 \Rightarrow c = \sqrt 2 $

$ \Rightarrow $ Tiêu điểm ${F_1}( - \sqrt 2 ;0),\,\,{F_2}(\sqrt 2 ;0)$.

$(H):\,\,16{x^2} - 9{y^2} = 16 $ $\Leftrightarrow \dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{{\dfrac{{16}}{9}}} = 1 $ $\Rightarrow a = 1,\,\,b = \dfrac{4}{3}$

Hai đường tiệm cận của $(H):$ $y = \dfrac{b}{a}x = \dfrac{{\dfrac{4}{3}}}{1}x = \dfrac{4}{3}x;$

$y=  - \dfrac{b}{a}x =  - \dfrac{{\dfrac{4}{3}}}{1}x =  - \dfrac{4}{3}x$

$(H):\,\,9{x^2} - 16{y^2} = 144 \Leftrightarrow \dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{9} = 1 \Rightarrow a = 4,\,\,b = 3$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {c^2} = {4^2} + {3^2} = 25 \Rightarrow c = 5$

Tâm sai $e = \dfrac{c}{a} = \dfrac{5}{4}$.

$(H)$ có tiêu điểm ${F_2}(5;0)$ và đỉnh $A( - 4;0)$ $ \Rightarrow c = 5,\,\,a = 4$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {4^2} + {b^2} = {5^2} \Rightarrow b = 3$

Phương trình chính tắc của $(H):$ $\dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{9} = 1$

$(H)$ có trục thực, trục ảo dài lần lượt là $10$ và $6$ $ \Rightarrow a = 5,\,\,b = 3$

Phương trình chính tắc của $(H):$ $\dfrac{{{x^2}}}{{25}} - \dfrac{{{y^2}}}{9} = 1$

$(H)$ có trục thực dài bằng $8$ và tâm sai $e = \dfrac{5}{4}$$ \Rightarrow a = 4,\,\,e = \dfrac{c}{a} = \dfrac{5}{4} $ $\Rightarrow c = \dfrac{5}{4}.a = \dfrac{5}{4}.4 = 5$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {4^2} + {b^2} = {5^2} \Rightarrow b = 3$

Phương trình chính tắc của $(H):$ $\dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{9} = 1$.

$(H)$ có tiêu cự bằng $16$ và tâm sai $e = \dfrac{4}{3}$ $ \Rightarrow c = 8,\,\,e = \dfrac{c}{a} = \dfrac{4}{3} $ $\Rightarrow a = \dfrac{3}{4}c = \dfrac{3}{4}.8 = 6$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {6^2} + {b^2} = {8^2} \Rightarrow {b^2} = 28$

Phương trình chính tắc của $(H):$ $\dfrac{{{x^2}}}{{36}} - \dfrac{{{y^2}}}{{28}} = 1$

Gọi phương trình chính tắc của hypebol $(H)$ là: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1,\,\,(a,\,b > 0)$

$(H)$ đi qua $A\left( {\sqrt {10} ;6} \right)$ $ \Rightarrow \dfrac{{10}}{{{a^2}}} - \dfrac{{36}}{{{b^2}}} = 1$  (1)

$(H)$ có tâm sai $e = \sqrt 5 $$ \Rightarrow \dfrac{c}{a} = \sqrt 5  \Leftrightarrow \dfrac{{{c^2}}}{{{a^2}}} = 5 \Leftrightarrow {c^2} = 5{a^2}$

Mà ${a^2} + {b^2} = {c^2} \Leftrightarrow {a^2} + {b^2} = 5{a^2} \Leftrightarrow {b^2} = 4{a^2}$. Thay vào (1), ta được:

$\dfrac{{10}}{{{a^2}}} - \dfrac{{36}}{{4{a^2}}} = 1 \Leftrightarrow \dfrac{1}{{{a^2}}} = 1 \Leftrightarrow {a^2} = 1$

$ \Rightarrow {b^2} = 4{a^2} = 4.1 = 4$

$ \Rightarrow $ Phương trình chính tắc của hypebol $(H):$ $\dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{4} = 1$

Gọi phương trình chính tắc của hypebol $(H)$ là: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1,\,\,(a,\,b > 0)$

Phương trình $2$ đường tiệm cận của $(H)$ là: $y =  \pm \dfrac{b}{a}x$

Vì góc hợp bởi tiệm cận và $Ox$ bằng ${45^0}$ $ \Rightarrow \dfrac{b}{a} = \tan {45^0} \Leftrightarrow \dfrac{b}{a} = 1 \Leftrightarrow \dfrac{{{b^2}}}{{{a^2}}} = 1 $ $\Leftrightarrow {b^2} = {a^2}$

Mà ${a^2} + {b^2} = {c^2} \Rightarrow {a^2} + {a^2} = {c^2} \Leftrightarrow 2{a^2} = {c^2} \Leftrightarrow \dfrac{{{c^2}}}{{{a^2}}} = 2 \Leftrightarrow \dfrac{c}{a} = \sqrt 2  \Leftrightarrow e = \sqrt 2 $

Gọi phương trình chính tắc của hypebol $(H)$ là: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1,\,\,(a,\,b > 0)$

$(H)$ có tâm sai $e = \dfrac{5}{3} \Rightarrow \dfrac{c}{a} = \dfrac{5}{3} \Leftrightarrow c = \dfrac{5}{3}a$

Mà ${a^2} + {b^2} = {c^2} \Rightarrow {a^2} + {b^2} = {\left( {\dfrac{5}{3}a} \right)^2} \Leftrightarrow {b^2} = \dfrac{{16}}{9}{a^2} \Leftrightarrow b = \dfrac{4}{3}a$ (1)

Vì diện tích của hình chữ nhật cơ sở là $48 $ đơn vị diện tích nên

$2a.2b = 48 \Leftrightarrow ab = 12$ (2)

Từ (1), (2), suy ra: $a.\dfrac{4}{3}a = 12 \Leftrightarrow {a^2} = 9$

Mà ${b^2} = \dfrac{{16}}{9}{a^2} = \dfrac{{16}}{9}.9 = 16$

Phương trình chính tắc của $(H):$  $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{{16}} = 1$

Gọi phương trình chính tắc của hypebol $(H)$ là: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1,\,\,(a,\,b > 0)$

Vì góc giữa hai đường tiệm cận của $(H)$ bằng ${60^0}$ $ \Rightarrow \dfrac{{\left| {{b^2} - {a^2}} \right|}}{{{a^2} + {b^2}}} = \cos {60^0} $ $\Leftrightarrow \dfrac{{\left| {{b^2} - {a^2}} \right|}}{{{a^2} + {b^2}}} = \dfrac{1}{2} $ $\Leftrightarrow \left[ \begin{array}{l}\dfrac{{{b^2} - {a^2}}}{{{a^2} + {b^2}}} = \dfrac{1}{2}\\\dfrac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}} = \dfrac{1}{2}\end{array} \right. $ $\Leftrightarrow \left[ \begin{array}{l}{b^2} = 3{a^2}\\{a^2} = 3{b^2}\end{array} \right.$

Ta có: ${a^2} + {b^2} = {c^2}$

TH1: ${b^2} = 3{a^2} \Rightarrow {a^2} + 3{a^2} = {c^2} \Leftrightarrow 4{a^2} = {c^2} \Leftrightarrow \dfrac{{{c^2}}}{{{a^2}}} = 4 \Leftrightarrow \dfrac{c}{a} = 2 \Leftrightarrow e = 2$

TH2:  ${a^2} = 3{b^2} \Leftrightarrow {b^2} = \dfrac{1}{3}{a^2}\,\,\,\, \Rightarrow {a^2} + \dfrac{1}{3}{a^2} = {c^2} \Leftrightarrow \dfrac{4}{3}{a^2} = {c^2} \Leftrightarrow \dfrac{{{c^2}}}{{{a^2}}} = \dfrac{4}{3} \Leftrightarrow \dfrac{c}{a} = \dfrac{2}{{\sqrt 3 }} \Leftrightarrow e = \dfrac{2}{{\sqrt 3 }}$

Vậy, $e = 2$ hoặc $e = \dfrac{2}{{\sqrt 3 }}$

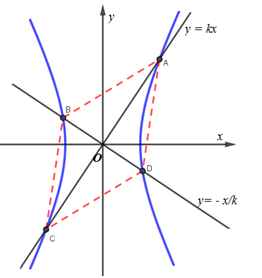
Giả sử phương trình đường thẳng $AC$ là \(y = kx\)

Tọa độ của $A$ là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}y = kx\\\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = kx\\\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{k^2}{x^2}}}{{{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y^2} = {k^2}{x^2}\\{x^2}\left( {\dfrac{1}{{{a^2}}} - \dfrac{{{k^2}}}{{{b^2}}}} \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \dfrac{{{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}}\\{y^2} = \dfrac{{{k^2}{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}}\end{array} \right.\)

\( \Rightarrow O{A^2} = {x^2} + {y^2} = \dfrac{{{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} + \dfrac{{{k^2}{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} = \dfrac{{\left( {1 + {k^2}} \right){a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} \Rightarrow \dfrac{1}{{O{A^2}}} = \dfrac{{{b^2} - {k^2}{a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}\)

Chứng minh tương tự ta được \(O{B^2} = \dfrac{{\left( {1 + {k^2}} \right){a^2}{b^2}}}{{{k^2}{b^2} - {a^2}}} \Rightarrow \dfrac{1}{{O{B^2}}} = \dfrac{{{k^2}{b^2} - {a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}\)

\(\begin{array}{l} \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{{{b^2} - {k^2}{a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}} + \dfrac{{{k^2}{b^2} - {a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}\\ = \dfrac{{{b^2}\left( {1 + {k^2}} \right) - {a^2}\left( {1 + {k^2}} \right)}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}} = \dfrac{{{b^2} - {a^2}}}{{{a^2}{b^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{{b^2}}} = const\end{array}\) 

Khi đó:

$\begin{array}{l}\dfrac{1}{{{a^2}}} - \dfrac{1}{{{b^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\mathop  \ge \limits^{Cauchy} \dfrac{2}{{OA.OB}} = \dfrac{4}{{{S_{ABCD}}}}\\ \Leftrightarrow \dfrac{{{b^2} - {a^2}}}{{{a^2}{b^2}}} \ge \dfrac{4}{{{S_{ABCD}}}} \Leftrightarrow {S_{ABCD}} \ge \dfrac{{4{a^2}{b^2}}}{{{b^2} - {a^2}}}\\ \Rightarrow {S_{ABCD\,Min}} = \dfrac{{4{a^2}{b^2}}}{{{b^2} - {a^2}}} \Leftrightarrow OA = OB\end{array}$

$ \Leftrightarrow \Delta OAB$ vuông cân tại $O$

$ \Rightarrow y = kx$ là tia phân giác của góc phần tư thứ $I$

$ \Rightarrow k = 1$