Trong các đẳng thức sau đây, đẳng thức nào đúng ?
Vì \(\alpha = {150^0}\) là góc tù nên \(\sin \alpha > 0,\cos \alpha < 0,\tan \alpha = \dfrac{{\sin \alpha }}{{c{\rm{os}}\alpha }} < 0,\cot \alpha < 0.\)
Do đó các đáp án A, B, D đều sai. Ta chỉ xét đáp án C. Ta có \(\tan {150^ \circ } = - \tan {30^ \circ } = - \dfrac{1}{{\sqrt 3 }}.\)
Cho tam giác ABC, có BC = a, CA = b, AB = c. Mệnh đề nào sau đây đúng?
Nếu \(\cos A > 0\) thì góc A nhọn hay \({b^2} + {c^2} - {a^2} > 0\) thì góc A nhọn.
Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C = - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.
Áp dụng định lí cosin trong tam giác \(ABC\) ta có:
\({c^2} = {a^2} + {b^2} - 2a.b.\cos C\)\( \Rightarrow 81 = 25 + {b^2} - 2.5.b.\left( { - \dfrac{1}{{10}}} \right)\)\( \Leftrightarrow {b^2} - b - 56 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}b = 7\\b = - 8\end{array} \right.\)
Ta nhận được \(b = 7({\rm{cm}})\)
Diện tích tam giác \(ABC\) là \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)\( = \sqrt {\dfrac{{21}}{2}\left( {\dfrac{{21}}{2} - 5} \right)\left( {\dfrac{{21}}{2} - 7} \right)\left( {\dfrac{{21}}{2} - 9} \right)} \)\( = \dfrac{{21\sqrt {11} }}{4}({\rm{c}}{{\rm{m}}^2})\)
Độ dài đường cao \({h_a} = \dfrac{{2S}}{a}\)\( = \dfrac{{\dfrac{{21\sqrt {11} }}{2}}}{5}\)\( = \dfrac{{21\sqrt {11} }}{{10}}({\rm{cm}})\)
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) thỏa mãn \(MO = 3R\). Một đường kính \(AB\) thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức \(S = MA + MB\).
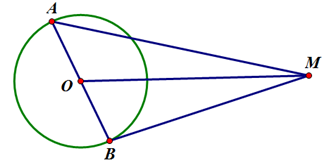
Gọi \(\widehat {MOA} = \alpha \Rightarrow \widehat {MOB} = 180^\circ - \alpha \).
Ta có \(MA = \sqrt {M{O^2} + A{O^2} - 2MO.AO.\cos \alpha } = \sqrt {9{R^2} + {R^2} - 6{R^2}\cos \alpha } = R\sqrt {10 - 6\cos \alpha } \).
\(MB = \sqrt {M{O^2} + B{O^2} - 2MO.BO.\cos \left( {180^\circ - \alpha } \right)} = \sqrt {9{R^2} + {R^2} + 6{R^2}\cos \alpha } = R\sqrt {10 + 6\cos \alpha } \).
Xét \(C = \sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } \) \( \Rightarrow {C^2} = 20 + 2\sqrt {100 - 36{{\cos }^2}\alpha } \ge 20 + 2\sqrt {100 - 36} = 36\).
Suy ra \(C \ge 6\). Dấu xẩy ra khi ${\cos ^2}\alpha = 1 \Leftrightarrow \left[ \begin{array}{l}\cos \alpha = 1\\\cos \alpha = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = 0^\circ \\\alpha = 180^\circ \end{array} \right.$.
Ta có $S = MA + MB = R\left( {\sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } } \right) \ge 6R$.
Suy ra \(\min S = 6R\) khi và chỉ khỉ \(A\), \(O\), \(B\), \(M\) thẳng hàng.
Cho hình thang cân \(ABCD\) có đáy nhỏ \(AB\), đáy lớn \(CD\). Biết \(AB = AD\) và \(\tan \widehat {BDC} = \dfrac{3}{4}\). Tính $\cos \widehat {BAD}$.
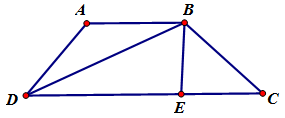
Gọi $E$ là hình chiếu vuông góc của \(B\) trên $DC$. Đặt $AB = AD = BC = x$.
Ta có \(EC = \dfrac{{DC - x}}{2}\) \(\left( 1 \right)\).
Trong tam giác vuông \(BDE\) ta có: \(\tan \widehat {BDC} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(\dfrac{{BE}}{{ED}} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(BE = \dfrac{3}{4}ED\)
\( \Leftrightarrow \) \(BE = \dfrac{3}{4}\left( {DC - \dfrac{{DC - x}}{2}} \right)\)\( = \dfrac{3}{8}\left( {DC + x} \right)\) \(\left( 2 \right)\).
Trong tam giác vuông \(BEC\) ta có \(B{C^2} = E{C^2} + B{E^2}\) \(\left( 3 \right)\).
Thay \(\left( 1 \right)\), \(\left( 2 \right)\) vào \(\left( 3 \right)\) biến đổi ta được: \(39{x^2} + 14DC.\,x - 25D{C^2} = 0\) \( \Leftrightarrow \) \(x = \dfrac{{25}}{{39}}DC\) hay \(DC = \dfrac{{39}}{{25}}x\). Khi đó \(EC = \dfrac{7}{{25}}x\).
Mặt khác: $\cos \widehat {BAD}$\( = - \cos \widehat {BCE}\)\( = - \dfrac{{EC}}{{BC}} = - \dfrac{7}{{25}}\)
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \({60^0}\). Tàu thứ nhất chạy với tốc độ \(30\,km/h\), tàu thứ hai chạy với tốc độ \(40\,km/h\). Hỏi sau \(2\) giờ hai tàu cách nhau bao nhiêu \(km\)?

Ta có: Sau \(2h\) quãng đường tàu thứ nhất chạy được là: \({S_1} = 30.2 = 60\,km.\)
Sau \(2h\) quãng đường tàu thứ hai chạy được là: \({S_2} = 40.2 = 80\,km.\)
Vậy: sau \(2h\) hai tàu cách nhau là: \(S = \sqrt {{S_1}^2 + {S_2}^2 - 2{S_1}.{S_2}.\cos {{60}^0}} = 20\sqrt {13} .\)
Xác định dạng của tam giác $ABC$ biết rằng $S = \dfrac{{\sqrt 3 }}{{36}}{\left( {a + b + c} \right)^2}$
Theo công thức He-rong ta có
$\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{\sqrt 3 }}{9}{p^2} \Leftrightarrow \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) = \dfrac{1}{{27}}{p^3}$
Theo bất đẳng thức Cauchy ta có $\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \le \dfrac{{{{\left( {p - a + p - b + p - c} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - \left( {a + b + c} \right)} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - 2p} \right)}^3}}}{{27}} = \dfrac{{{p^3}}}{{27}}$
Đẳng thức xảy ra khi a = b = c.
Khi đó tam giác $ABC$ đều.
Tìm bán kính đường tròn ngoại tiếp tam giác $ABC $ biết $ b = 7cm,\,\,c = 5 cm,\,\,{\mathop{\rm cosA}\nolimits} = \dfrac{3}{5}$.
Theo định lí cosin ta có ${a^2} = {b^2} + {c^2} - 2bc\cos A = {7^2} + {5^2} - 2.7.5.\dfrac{3}{5} = 32 \Rightarrow a = 4\sqrt 2 $
Từ công thức ${\sin ^2}A + {\cos ^2}A = 1 \Rightarrow {\mathop{\rm sinA}\nolimits} = \dfrac{4}{5}$
Theo định lí sin ta có $\dfrac{a}{{\sin A}} = 2R \Rightarrow R = \dfrac{a}{{2\sin A}} = \dfrac{{4\sqrt 2 }}{{2.\dfrac{4}{5}}} = \dfrac{{5\sqrt 2 }}{2}$.
Xác định hình dạng tam giác $ABC$ biết $\left\{ \begin{array}{l}\dfrac{{{b^3} + {c^3} - {a^3}}}{{b + c - a}} = {a^2}\\a = 2b\cos C\end{array} \right.$
Theo định lí cosin ta có ${\mathop{\rm cosC}\nolimits} = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$, thay vào đẳng thức thứ hai của hệ trên ta có
$a = 2b{\mathop{\rm cosC}\nolimits} = 2b.\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \Rightarrow {a^2} = {a^2} + {b^2} - {c^2} \Leftrightarrow {b^2} - {c^2} = 0 \Leftrightarrow {b^2} = {c^2} \Rightarrow b = c$
Thay b = c vào hệ thức thứ nhất ta có $\dfrac{{2{b^3} - {a^3}}}{{2b - a}} = {a^2} \Leftrightarrow 2{b^3} - {a^3} = 2b{a^2} - {a^3} \Leftrightarrow {b^2} = {a^2} \Rightarrow a = b$
Do đó a = b = c. Vậy tam giác $ABC$ đều.
Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4 m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.
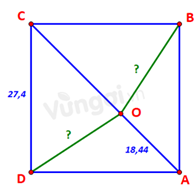
Ta có: \( CD = 27,4 \Rightarrow AC = CD.\sqrt 2 = 27,4.\sqrt 2 \approx 38,75\)
\( \Rightarrow OC = AC - OA \approx 38,75 - 18,44 = 20,31\)
Xét tam giác OCD ta có:
Định lí cos: \( O{D^2} = C{D^2} + C{O^2} - 2.CD.CO.\cos C\)
Trong đó \( \left\{ \begin{array}{l}CD = 27,4\\CO = 20,31\\\widehat C = {45^o}\end{array} \right.\)
\( \begin{array}{l} \Rightarrow O{D^2} = 27,{4^2} + 20,{31^2} - 2.27,4.20,31.\cos {45^o}\\ \Leftrightarrow O{D^2} \approx 376,255\\ \Leftrightarrow OD \approx 19,4\;(m)\end{array}\)
Dễ thấy \( \Delta \,COB = \Delta \,COD\)(c.g.c) \( \Rightarrow OB = OD = 19,4\;(m)\)
Cho tam giác ABC có trung tuyến AM. Chọn khẳng định đúng
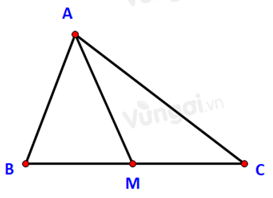
Ta có: \( \widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \( \cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
Tính giá trị của các biểu thức sau:
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \( \left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \dfrac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \dfrac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \( M = \dfrac{{\sqrt 2 }}{2}.\dfrac{{\sqrt 2 }}{2} + \dfrac{1}{2} = \dfrac{2}{4} + \dfrac{1}{2} = 1\)
Điền dấu ">,<,=" vào chỗ trống:
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
\( \Rightarrow {b^2} + {c^2} - {a^2} = 2bc\;\cos A\)(1)
Mặt khác, xét nửa đường tròn đường giác:
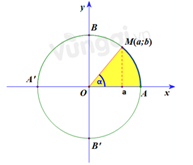
Ta có: \( \cos \alpha = a\) với a là hoành độ của điểm M.
Dễ dàng suy ra:
Nếu góc A nhọn thì \( \cos A > 0\)
Từ (1), suy ra \( {b^2} + {c^2} - {a^2} = 2bc\;\cos A > 0\)
Hay \( {b^2} + {c^2} > {a^2}\)

