Số nghiệm của phương trình \(2x + \dfrac{2}{{\sqrt {x + 2} }} = - {x^2} + \dfrac{2}{{\sqrt {x + 2} }}\) là:
Điều kiện : \(x > - 2\) .
\(2x + \dfrac{2}{{\sqrt {x + 2} }} = - {x^2} + \dfrac{2}{{\sqrt {x + 2} }}\)
\( \Rightarrow \) \(2x = - {x^2} \Leftrightarrow x\left( {x + 2} \right) = 0 \) \(\Rightarrow \left[ \begin{array}{l}x = 0\\x = - 2(loai)\end{array} \right.\) .
Kết hợp với điều kiện ta được \(x = 0\) là nghiệm duy nhất.
Có tất cả bao nhiêu giá trị nguyên không dương của tham số $m$ để phương trình $\sqrt {2x + m} = x - 1$ có nghiệm duy nhất?
$\sqrt {2x + m} = x - 1$$ \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\2x + m = {\left( {x - 1} \right)^2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 4x + 1 - m = 0\left( * \right)\end{array} \right.$.
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
Xét ${x^2} - 4x + 1 - m = 0$; \(\Delta ' = 3 + m\)
TH1: \(\Delta ' = 0 \Leftrightarrow m = - 3\) thì (*) có nghiệm kép \(x = 2 \ge 1\) (thỏa).
TH2: \(\Delta ' > 0 \Leftrightarrow m > - 3\) thì phương trình có nghiệm duy nhất khi (*) có 2 nghiệm thỏa \({x_1} < 1 < {x_2}\) \( \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) < 0 \Leftrightarrow {x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 < 0\) \( \Leftrightarrow 1 - m - 4 + 1 < 0 \Leftrightarrow m > - 2\).
Do $m$ không dương nên $m\in \{-1;0\}$
Kết hợp với trường hợp $m=-3$ ở trên ta được $3$ giá trị của $m$ thỏa mãn bài toán.
Nghiệm của phương trình \(\sqrt {2x - 7} = 1\) là
Điều kiện: \(x \ge \dfrac{7}{2}\) .
\(\sqrt {2x - 7} = 1\) \( \Rightarrow \) \(2x - 7 = 1 \Leftrightarrow x = 4\) .
Kết hợp với điều kiện ta được \(x = 4\) là nghiệm duy nhất..
Tập xác định của phương trình \(\dfrac{{\sqrt {3x + 5} }}{{{x^2} + 1}} = \dfrac{2}{{\sqrt {2 - x} }}\) là
Điều kiện xác định \(\left\{ {\begin{array}{*{20}{c}}{3x + 5 \ge 0}\\{2 - x > 0}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - \dfrac{5}{3}\\x < 2\end{array} \right. \Leftrightarrow - \dfrac{5}{3} \le x < 2\).
Điều kiện xác định của phương trình \(\dfrac{{\sqrt {x + 2} }}{x} = \dfrac{2}{{{x^2} + 3x - 4}}\) là
Điều kiện xác định \(\left\{ {\begin{array}{*{20}{c}}{x + 2 \ge 0}\\{x \ne 0}\\{{x^2} + 3x - 4 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 1\\x \ne 0\\x \ne - 4\end{array} \right. \Leftrightarrow \) \(x \in \left[ { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\).
Số nghiệm của phương trình \(\sqrt {{x^2} + 2x + 4} = 2\) là
Ta có \(\sqrt {{x^2} + 2x + 4} = 2 \Leftrightarrow {x^2} + 2x + 4 = 4 \Leftrightarrow x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\).
Có bao nhiêu giá trị $m$ nguyên để phương trình \(\sqrt {x + 2} + \sqrt {2 - x} + 2\sqrt { - {x^2} + 4} - 2m + 3 = 0\) có nghiệm.
Đặt \(t = \sqrt {x + 2} + \sqrt {2 - x} \)
Điều kiện \(t = \sqrt {x + 2} + \sqrt {2 - x} \ge \sqrt {x + 2 + 2 - x} = 2 \Rightarrow t \ge 2\)
Lại có \(\sqrt {x + 2} + \sqrt {2 - x} \le \sqrt {{1^2} + {1^2}} .\sqrt {x + 2 + 2 - x} = 2\sqrt 2 \) \( \Rightarrow t \le 2\sqrt 2 \)
Suy ra \(2 \le t \le 2\sqrt 2 \)
Ta có: \({t^2} = 4 + 2\sqrt {4 - {x^2}} \)\( \Rightarrow 2\sqrt {4 - {x^2}} = {t^2} - 4\)
Phương trình trở thành: \(t + {t^2} - 4 - 2m + 3 = 0\)\( \Leftrightarrow {t^2} + t - 2m - 1 = 0\)\( \Leftrightarrow {t^2} + t - 1 = 2m\,\,\,(*)\)
Xét hàm số \(f\left( t \right) = {t^2} + t - 1\) (parabol có hoành độ đỉnh \(x = - \dfrac{1}{2} \notin \left[ {2;2\sqrt 2 } \right]\)) trên \(\left[ {2;2\sqrt 2 } \right]\), có bảng biến thiên
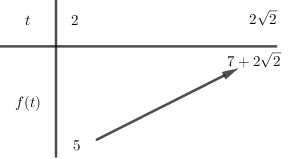
Phương trình $(*)$ có nghiệm thỏa \(2 \le t \le 2\sqrt 2 \) khi \(5 \le 2m \le 7 + 2\sqrt 2 \)\( \Rightarrow \dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\)
\(\dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\,\)\( \to \left( {2,5 \le m \le 4,91} \right)\)
Vậy có 2 giá trị \(m\) nguyên dương là \(m = 3\), \(m = 4\).
Có bao nhiêu giá trị nguyên của m để phương trình \({x^2} - 4\sqrt {{x^2} + 1} - \left( {m - 1} \right) = 0\) có \(4\) nghiệm phân biệt
Điều kiện xác định \(x \in \mathbb{R}\).
Đặt \(t = \sqrt {{x^2} + 1} \), \(t \ge 1\).
Phương trình trở thành \({t^2} - 1 - 4t - m + 1 = 0\)\( \Leftrightarrow {t^2} - 4t = m\). \(\left( 2 \right)\)
Để phương trình có \(4\) nghiệm phân biệt thì phương trình \(\left( 2 \right)\) có hai nghiệm phân biệt lớn hơn \(1\).
Xét hàm số \(f\left( t \right) = {t^2} - 4t\) có đồ thị là parabol có hoành độ đỉnh \(x = 2 \in \left( {1; + \infty } \right)\) nên ta có bảng biến thiên:
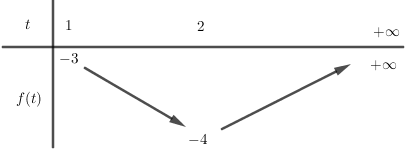
Dựa BBT ta thấy để $(2)$ có hai nghiệm phân biệt lớn hơn $1$ thì \( - 4 < m < - 3\).
Vậy không có giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Tìm các giá trị của \(m\) để phương trình \(2\sqrt {x + 1} = x + m\) có nghiệm:
\(2\sqrt {x + 1} = x + m\)\(\left( 1 \right)\)
Phương trình tương đương: \(\left\{ \begin{array}{l}x + m \ge 0\\4\left( {x + 1} \right) = {x^2} + 2mx + {m^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - m\\{x^2} + 2\left( {m - 2} \right)x + {m^2} - 4 = 0\left( 2 \right)\end{array} \right.\)
Phương trình \(\left( 2 \right)\) có nghiệm \( \Leftrightarrow {\rm{pt}}\left( 2 \right)\)có ít nhất một nghiệm lớn hơn hoặc bằng \( - m\).
\(\Delta ' = 8 - 4m\)
Phương trình \(\left( 2 \right)\) có nghiệm \( \Leftrightarrow \Delta ' \ge 0\)\( \Leftrightarrow m \le 2\)
Khi đó phương trình \(\left( 2 \right)\) có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = 2 - m - \sqrt {8 - 4m} \\{x_2} = 2 - m + \sqrt {8 - 4m} \end{array} \right.\).
Dễ thấy \({x_2} = 2 - m + \sqrt {8 - 4m} > - m,\forall m \le 2\) nên \(\left( 2 \right)\) luôn có ít nhất \(1\) nghiệm \(x \ge - m\) thỏa mãn bài toán.
Vậy \(m \le 2\).
Số nghiệm nguyên dương của phương trình \(\sqrt {x - 1} = x - 3\) là:
\(\sqrt {x - 1} = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right. \Leftrightarrow x = 5\).
Phương trình \(\dfrac{4}{{\sqrt {2 - x} }} - \sqrt {2 - x} = 2\) có bao nhiêu nghiệm?
Điều kiện: \(x < 2.\)
$\begin{array}{l}{\rm{PT}} \Leftrightarrow 4 - \left( {2 - x} \right) = 2\sqrt {2 - x} \Leftrightarrow 2\sqrt {2 - x} = 2 + x \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\{\left( {x + 2} \right)^2} = 4\left( {2 - x} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\{x^2} + 8x - 4 = 0\end{array} \right.\\\,\,\,\,\,\, \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\\left[ \begin{array}{l}x = - 4 - 2\sqrt 5 \\x = - 4 + 2\sqrt 5 \end{array} \right.\end{array} \right. \Leftrightarrow x = - 4 + 2\sqrt 5 \Rightarrow S = \left\{ { - 4 + 2\sqrt 5 } \right\}.\end{array}$
Phương trình \(\sqrt {10x + 1} + \sqrt {3x - 5} = \sqrt {9x + 4} + \sqrt {2x - 2} {\rm{ }}\left( * \right)\) có nghiệm ${x_0}$ thỏa mãn
Điều kiện: \(x \ge \dfrac{5}{3}\).
\(\begin{array}{l}\left( * \right) \Leftrightarrow \left( {\sqrt {10x + 1} - \sqrt {9x + 4} } \right) + \left( {\sqrt {3x - 5} - \sqrt {2x - 2} } \right) = 0\\ \Leftrightarrow \dfrac{{10x + 1 - \left( {9x + 4} \right)}}{{\sqrt {10x + 1} + \sqrt {9x + 4} }} + \dfrac{{3x - 5 - \left( {2x - 2} \right)}}{{\sqrt {3x - 5} + \sqrt {2x - 2} }} = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {\dfrac{1}{{\sqrt {10x + 1} + \sqrt {9x + 4} }} + \dfrac{1}{{\sqrt {3x - 5} + \sqrt {2x - 2} }}} \right) = 0\end{array}\)
Vì \(\forall x \ge \dfrac{5}{3} \Rightarrow \dfrac{1}{{\sqrt {10x + 1} + \sqrt {9x + 4} }} + \dfrac{1}{{\sqrt {3x - 5} + \sqrt {2x - 2} }} > 0\) nên \(\left( 1 \right) \Leftrightarrow x = 3\).
Kết hợp điều kiện phương trình có nghiệm duy nhất \(x = 3\).
Tính tổng các nghiệm của phương trình \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\)
ĐK: \(x \ge \dfrac{{ - 7}}{2}\)
Ta có \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 2} \right)\sqrt {2x + 7} = \left( {x - 2} \right)\left( {x + 2} \right)\\ \Leftrightarrow \left( {x - 2} \right)\left[ {\sqrt {2x + 7} - \left( {x + 2} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\sqrt {2x + 7} = x + 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}2x + 7 = {\left( {x + 2} \right)^2}\\x \ge - 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\2x + 7 = {x^2} + 4x + 4\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\{x^2} + 2x - 3 = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = 1\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Tổng hai nghiệm của phương trình là: \(2 + 1 = 3.\)

