Có bao nhiêu giá trị $m$ nguyên để phương trình \(\sqrt {x + 2} + \sqrt {2 - x} + 2\sqrt { - {x^2} + 4} - 2m + 3 = 0\) có nghiệm.
Trả lời bởi giáo viên
Đặt \(t = \sqrt {x + 2} + \sqrt {2 - x} \)
Điều kiện \(t = \sqrt {x + 2} + \sqrt {2 - x} \ge \sqrt {x + 2 + 2 - x} = 2 \Rightarrow t \ge 2\)
Lại có \(\sqrt {x + 2} + \sqrt {2 - x} \le \sqrt {{1^2} + {1^2}} .\sqrt {x + 2 + 2 - x} = 2\sqrt 2 \) \( \Rightarrow t \le 2\sqrt 2 \)
Suy ra \(2 \le t \le 2\sqrt 2 \)
Ta có: \({t^2} = 4 + 2\sqrt {4 - {x^2}} \)\( \Rightarrow 2\sqrt {4 - {x^2}} = {t^2} - 4\)
Phương trình trở thành: \(t + {t^2} - 4 - 2m + 3 = 0\)\( \Leftrightarrow {t^2} + t - 2m - 1 = 0\)\( \Leftrightarrow {t^2} + t - 1 = 2m\,\,\,(*)\)
Xét hàm số \(f\left( t \right) = {t^2} + t - 1\) (parabol có hoành độ đỉnh \(x = - \dfrac{1}{2} \notin \left[ {2;2\sqrt 2 } \right]\)) trên \(\left[ {2;2\sqrt 2 } \right]\), có bảng biến thiên
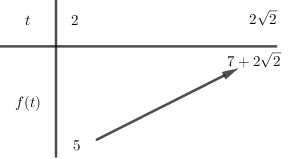
Phương trình $(*)$ có nghiệm thỏa \(2 \le t \le 2\sqrt 2 \) khi \(5 \le 2m \le 7 + 2\sqrt 2 \)\( \Rightarrow \dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\)
\(\dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\,\)\( \to \left( {2,5 \le m \le 4,91} \right)\)
Vậy có 2 giá trị \(m\) nguyên dương là \(m = 3\), \(m = 4\).
Hướng dẫn giải:
- Đặt \(t = \sqrt {x + 2} + \sqrt {2 - x} \), tìm diều kiện của \(t\)
- Đưa phương trình về bậc hai ẩn \(t\) rồi tìm điều kiện để phương trình có nghiệm \(t\) thỏa mãn điều kiện vừa tìm được.

