Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm $A$ và $B$ trên mặt đất có khoảng cách $AB = 12\,{\rm{m}}$ cùng thẳng hàng với chân $C$ của tháp để đặt hai giác kế. Chân của giác kế có chiều cao $h = 1,3\,{\rm{m}}$. Gọi $D$ là đỉnh tháp và hai điểm \({A_1}\), \({B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao $CD$ của tháp. Người ta đo được góc \(\widehat {D{A_1}{C_1}} = 49^\circ \) và \(\widehat {D{B_1}{C_1}} = 35^\circ \). Tính chiều cao $CD$ của tháp.

Ta có $\widehat {{C_1}D{A_1}} = 90^\circ - 49^\circ = 41^\circ $; $\widehat {{C_1}D{B_1}} = 90^\circ - 35^\circ = 55^\circ $, nên $\widehat {{A_1}D{B_1}} = 14^\circ $.
Xét tam giác ${A_1}D{B_1}$, có $\dfrac{{{A_1}{B_1}}}{{\sin \widehat {{A_1}D{B_1}}}} = \dfrac{{{A_1}D}}{{\sin \widehat {{A_1}{B_1}D}}}$$ \Rightarrow {A_1}D = \dfrac{{12.\sin 35^\circ }}{{\sin 14^\circ }}$$ \approx 28,45\,{\rm{m}}$.
Xét tam giác ${C_1}{A_1}D$ vuông tại ${C_1}$, có
$\sin \widehat {{C_1}{A_1}D} = \dfrac{{{C_1}D}}{{{A_1}D}}$$ \Rightarrow {C_1}D = {A_1}D.\sin {C_1}{A_1}D = 28,45.\sin 49^\circ $$ \approx 21,47\,{\rm{m}}$$ \Rightarrow CD = {C_1}D + C{C_1} \approx 22,77{\rm{ m}}$.
Trên nóc một tòa nhà có cột ăng-ten cao \(5\,{\rm{m}}\). Từ vị trí quan sát \(A\) cao \(7\,{\rm{m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là:

Ta có chiều cao của tòa nhà chính là đoạn \(BH\).
Mà \(BH = CD + DH\)\( = CD + 7\).
Xét tam giác \(ACD\) vuông tại \(D\) có \(AC = \dfrac{{CD}}{{\sin 40^\circ }}\)
Xét tam giác \(ABD\) vuông tại \(D\) có \(AB = \dfrac{{5 + CD}}{{\sin 50^\circ }}\)
Xét tam giác \(ABC\) có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)
\( \Leftrightarrow \left( {\dfrac{1}{{{{\sin }^2}50^\circ }} + \dfrac{1}{{{{\sin }^2}40^\circ }} - \dfrac{{2\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)C{D^2} + \left( {\dfrac{{10}}{{{{\sin }^2}50^\circ }} - \dfrac{{10\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)CD + \dfrac{{25}}{{{{\sin }^2}50^\circ }} - 25 = 0\)\( \Leftrightarrow CD \approx 11,9\)
\( \Rightarrow BC \approx 7 + 11,9\)\( \approx 18,9\) (m).
Vậy tòa nhà cao \(18,9{\rm{ m}}\).
Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C = - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.
Áp dụng định lí cosin trong tam giác \(ABC\) ta có:
\({c^2} = {a^2} + {b^2} - 2a.b.\cos C\)\( \Rightarrow 81 = 25 + {b^2} - 2.5.b.\left( { - \dfrac{1}{{10}}} \right)\)\( \Leftrightarrow {b^2} - b - 56 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}b = 7\\b = - 8\end{array} \right.\)
Ta nhận được \(b = 7({\rm{cm}})\)
Diện tích tam giác \(ABC\) là \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)\( = \sqrt {\dfrac{{21}}{2}\left( {\dfrac{{21}}{2} - 5} \right)\left( {\dfrac{{21}}{2} - 7} \right)\left( {\dfrac{{21}}{2} - 9} \right)} \)\( = \dfrac{{21\sqrt {11} }}{4}({\rm{c}}{{\rm{m}}^2})\)
Độ dài đường cao \({h_a} = \dfrac{{2S}}{a}\)\( = \dfrac{{\dfrac{{21\sqrt {11} }}{2}}}{5}\)\( = \dfrac{{21\sqrt {11} }}{{10}}({\rm{cm}})\)
Từ một miếng tôn có hình dạng là nửa đường tròn bán kính $1\;{\rm{m}}$, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?


Xét đường tròn bán kính $1$, ta cắt trên đó một hình chữ nhật $ABCD$.
Khi đó ${S_{ABCD}} = \dfrac{1}{2}AC.BD.\sin \alpha $$ = 2\sin \alpha \le 2$.
Dấu bằng xảy ra khi và chỉ khi $\alpha = 90^\circ $.
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng $1$.
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
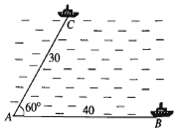
Sau \(2\) giờ tàu \(B\) đi được \(40\) hải lí, tàu \(C\) đi được \(30\) hải lí. Vậy tam giác \(ABC\) có \(AB = 40,\,\,\,AC = 30\) và \(\widehat A = {60^0}.\)
Áp dụng định lí côsin vào tam giác \(ABC,\) ta có
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)\( = {30^2} + {40^2} - 2.30.40.\cos {60^0}\)\( = 900 + 1600 - 1200 = 1300\)
Vậy \(BC = \sqrt {1300} \approx 36\) (hải lí).
Sau \(2\) giờ, hai tàu cách nhau khoảng \(36\) hải lí.
Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).
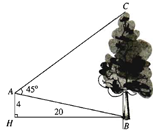
Biết \(AH = 4{\rm{m}},{\rm{ }}HB = 20{\rm{m}},{\rm{ }}\widehat {BAC} = {45^0}\).
Chiều cao của cây gần nhất với giá trị nào sau đây?
Trong tam giác \(AHB\), ta có \(\tan \widehat {ABH} = \dfrac{{AH}}{{BH}} = \dfrac{4}{{20}} = \dfrac{1}{5}\) \( \Rightarrow \widehat {ABH} \approx {11^0}19\)
Suy ra \(\widehat {ABC} = {90^0} - \widehat {ABH} = {78^0}41'\).
Suy ra \(\widehat {ACB} = {180^0} - \left( {\widehat {BAC} + \widehat {ABC}} \right) = {56^0}19'\).
Áp dụng định lý sin trong tam giác \(ABC\), ta được \(\dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{CB}}{{\sin \widehat {BAC}}}\)\( \Rightarrow CB = \dfrac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} \approx 17{\rm{m}}\)
Cho tam giác ABC có \( \widehat B = {135^o}\). Khẳng định nào sau đây là đúng?
Công thức tính diện tích là:
Ta có:
Công thức tính diện tích là: \( S = \dfrac{1}{2}ac.\sin B\)
Mà \( \widehat B = {135^o} \Rightarrow \sin B = \sin {135^o} = \dfrac{{\sqrt 2 }}{2}\).
Thay vào công thức tính diện tích, ta được:
\( S = \dfrac{1}{2}ac.\dfrac{{\sqrt 2 }}{2} = \dfrac{{\sqrt 2 }}{4}.ac\)
Cho tam giác ABC có \( \widehat B = {135^o}\). Khẳng định nào sau đây là đúng?
Bán kính đường tròn ngoại tiếp \(R\) là:
Theo định lí sin, ta có: \( R = \dfrac{a}{{2\sin A}} = \dfrac{b}{{2\sin B}} = \dfrac{c}{{2\sin C}}\)
\( R = \dfrac{a}{{\sin A}}\) sai.
\( R = \dfrac{{\sqrt 2 }}{2}b\)
Mà \( \sin B = \dfrac{{\sqrt 2 }}{2} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{b}{\sqrt 2} =\dfrac{{\sqrt 2 }}{2}b \)
Vậy B đúng.
\( R = \dfrac{{\sqrt 2 }}{2}c\) (Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)
\( R = \dfrac{{\sqrt 2 }}{2}a\) (Loại vì không có dữ kiện về góc A nên không thể tính R theo a.)
Cho tam giác ABC có \( \widehat B = {135^o}\). Khẳng định nào sau đây là đúng?
\( {a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \( {a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
\( \dfrac{b}{{\sin A}} = \dfrac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \( \dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}\)
\( \sin B = \dfrac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \( \sin B = \dfrac{{\sqrt 2 }}{2}\))
\( {b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\( {b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \( \widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \( {b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
Vậy D đúng.
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A.\( S = \dfrac{{abc}}{{4r}}\)
Ta có: \( S = \dfrac{{abc}}{{4R}}\). Mà \( r < R\)nên suy ra \( S = \dfrac{{abc}}{{4R}} < \dfrac{{abc}}{{4r}}\)
Vậy A sai.
B.\( r = \dfrac{{2S}}{{a + b + c}}\)
Ta có: \( S = pr \Rightarrow r = \dfrac{S}{p}\)
Mà\( p = \dfrac{{a + b + c}}{2}\;\; \Rightarrow r = \dfrac{S}{p}\; = \dfrac{S}{{\dfrac{{a + b + c}}{2}}} = \dfrac{{2S}}{{a + b + c}}\;\)
Vậy B đúng
C.\( {a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
Sai vì theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
D.\( S = r\,(a + b + c)\)
Sai vì \( S = pr = r.\dfrac{{a + b + c}}{2}\)
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
+ \( \sin A = \sin \,(B + C)\)
Ta có: \( \widehat A + \widehat B + \widehat C = {180^o}\)
\( \begin{array}{l} \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\ \Rightarrow \sin \,(B + C) = \sin A\end{array}\)
Vậy A đúng.
+ \( \cos A = \cos \,(B + C)\)
Sai vì \( \cos \,(B + C) = - \cos A\)(Do \( \widehat A + \widehat B + \widehat C = {180^o}\))
+ \( \;\cos A > 0\)
Không đủ dữ kiện để kết luận.
Nếu \( {0^o} < \widehat A < {90^o}\) thì \( \cos A > 0\)
Nếu \( {90^o} < \widehat A < {180^o}\) thì \( \cos A < 0\)
+ \( \sin A\,\, \le 0\)
Ta có \( S = \dfrac{1}{2}bc.\sin A > 0\)
Mà \( b,c > 0\)
\( \Rightarrow \sin A > 0\)
Vậy D sai.
Cho tam giác ABC có \( \widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\).
Tính \( R\).
Theo định lí sin: \( \dfrac{a}{{2\sin A}} = \dfrac{b}{{2\sin B}} = \dfrac{c}{{2\sin C}} = R\)
+) Ta có: \( R = \dfrac{b}{{2\sin B}}\)
Mà \( b = AC = 10,\;\;\widehat B = {60^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{60}^o}}} = \dfrac{{10}}{{\sqrt 3 }} = \dfrac{{10\sqrt 3 }}{3}.\)
Cho tam giác ABC có \( \widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\).
Tính \( a\).
Ta có: \( R = \dfrac{a}{{2\sin A}} \Rightarrow a =2R.\sin A\)
Mà \( R = \dfrac{{10\sqrt 3 }}{3},\) \(\widehat A = {180^o} - \left( {\widehat B + \;\widehat C} \right) \)\(= {180^o} - \left( {{{60}^o} + {{45}^o}} \right) = {75^o}\)
\( \Rightarrow a = \dfrac{{2.10\sqrt 3 }}{3}.\sin {75^o} \approx 11,154\)
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \( N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.

Hỏi tàu A cần phải chuyển động theo hướng nào?
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \( \dfrac{a}{{\sin \alpha }} = \dfrac{b}{{\sin B}}\)
Trong đó: \( \left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\( \begin{array}{l} \Rightarrow \dfrac{{30t}}{{\sin \alpha }} = \dfrac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \dfrac{{30t.\sin {{124}^o}}}{{50t}} = \dfrac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \( \alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \( {30^o}\).
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \( N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.

Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?
Xét tam giác ABC, ta có:
\( \begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\( \dfrac{a}{{\sin A}} = \dfrac{c}{{\sin C}} \Rightarrow a = \dfrac{{c.\sin A}}{{\sin C}}\)
Mà \( \left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \dfrac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\( \begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

