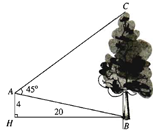
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm $A$ và $B$ trên mặt đất có khoảng cách $AB = 12\,{\rm{m}}$ cùng thẳng hàng với chân $C$ của tháp để đặt hai giác kế. Chân của giác kế có chiều cao $h = 1,3\,{\rm{m}}$. Gọi $D$ là đỉnh tháp và hai điểm \({A_1}\), \({B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao $CD$ của tháp. Người ta đo được góc \(\widehat {D{A_1}{C_1}} = 49^\circ \) và \(\widehat {D{B_1}{C_1}} = 35^\circ \). Tính chiều cao $CD$ của tháp.

Trên nóc một tòa nhà có cột ăng-ten cao \(5\,{\rm{m}}\). Từ vị trí quan sát \(A\) cao \(7\,{\rm{m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là:

Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C =  - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.

Từ một miếng tôn có hình dạng là nửa đường tròn bán kính $1\;{\rm{m}}$, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?

Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?

Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).

      Biết \(AH = 4{\rm{m}},{\rm{ }}HB = 20{\rm{m}},{\rm{ }}\widehat {BAC} = {45^0}\).

      Chiều cao của cây gần nhất với giá trị nào sau đây?

Cho tam giác ABC có \( \widehat B = {135^o}\). Khẳng định nào sau đây là đúng?

Công thức tính diện tích là: