Trả lời bởi giáo viên
Đáp án đúng: b
A.\( S = \dfrac{{abc}}{{4r}}\)
Ta có: \( S = \dfrac{{abc}}{{4R}}\). Mà \( r < R\)nên suy ra \( S = \dfrac{{abc}}{{4R}} < \dfrac{{abc}}{{4r}}\)
Vậy A sai.
B.\( r = \dfrac{{2S}}{{a + b + c}}\)
Ta có: \( S = pr \Rightarrow r = \dfrac{S}{p}\)
Mà\( p = \dfrac{{a + b + c}}{2}\;\; \Rightarrow r = \dfrac{S}{p}\; = \dfrac{S}{{\dfrac{{a + b + c}}{2}}} = \dfrac{{2S}}{{a + b + c}}\;\)
Vậy B đúng
C.\( {a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
Sai vì theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
D.\( S = r\,(a + b + c)\)
Sai vì \( S = pr = r.\dfrac{{a + b + c}}{2}\)
Hướng dẫn giải:
+) Định lí cos: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
+) Công thức tính diện tích: \( S = pr = \dfrac{{abc}}{{4R}}\)
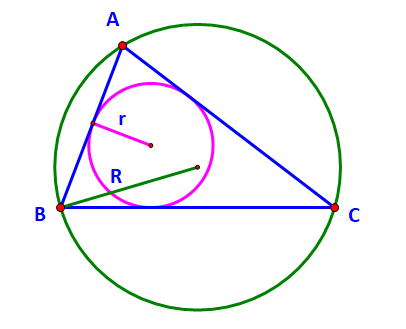
Trong đó: p là nửa chu vi,
R là bán kính đường tròn ngoại tiếp
r là bán kính đường tròn nội tiếp
Câu hỏi khác
- Bài tập trắc nghiệm Giải tam giác và ứng dụng thực tế môn Toán lớp 10 CTST có lời giải
- Bài tập trắc nghiệm Giá trị lượng giác của một góc từ 0 đến 180 môn Toán lớp 10 CTST có lời giải
- Bài tập trắc nghiệm Bài tập cuối chương IV môn Toán lớp 10 CTST có lời giải
- Bài tập trắc nghiệm Định lí côsin và định lí sin môn Toán lớp 10 CTST có lời giải
