Tìm tập xác định của hàm số$y = \dfrac{{x - 2}}{{{x^3} + {x^2} - 5x - 2}}$
ĐKXĐ: \({x^3} + {x^2} - 5x - 2 \ne 0\)\( \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 3x + 1} \right) \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 2}\\{x \ne \dfrac{{ - 3 \pm \sqrt 5 }}{2}}\end{array}} \right.\)
Suy ra tập xác định của hàm số là ${\rm{D}} = \mathbb{R}\backslash \left\{ {2;\dfrac{{ - 3 - \sqrt 5 }}{2};\dfrac{{ - 3 + \sqrt 5 }}{2}} \right\}$
Tìm tập xác định của hàm số $y = \dfrac{{\sqrt {x + 2} }}{{x\sqrt {{x^2} - 4x + 4} }}$
\(\left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\\begin{array}{l}{x^2} - 4x + 4 > 0\\x + 2 \ge 0\end{array}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\\begin{array}{l}{\left( {x - 2} \right)^2} > 0\\x \ge - 2\end{array}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\\begin{array}{l}x \ne 2\\x \ge - 2\end{array}\end{array}} \right.\)
Suy ra tập xác định của hàm số là ${\rm{D}} = \left[ { - 2; + \infty } \right)\backslash \left\{ {0;2} \right\}$.
Tìm tập xác định của hàm số$y = \left\{ \begin{array}{l}\dfrac{1}{x}\quad khi\;x \ge 1\\\sqrt {x + 1} \quad khi\;x < 1\end{array} \right.$
Khi \(x \ge 1\) thì hàm số là \(y = \dfrac{1}{x}\) luôn xác định với $x \ge 1$.
$=>$ ${D_1} = \left[ {1; + \infty } \right)$
Khi \(x < 1\) thì hàm số là \(y = \sqrt {x + 1} \) xác định khi
\(\left\{ {\begin{array}{*{20}{c}}{x < 1}\\{x + 1 \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x < 1}\\{x \ge - 1}\end{array}} \right.\\ \Leftrightarrow - 1 \le x < 1\)
$=>$${D_2} = \left[ { - 1;1} \right)$
Do đó hàm số đã cho có tập xác định $D = \left[ {1; + \infty } \right) \cup \left[ { - 1;1} \right) = \left[ { - 1; + \infty } \right)$
Cho hàm số: \(y = \dfrac{{mx}}{{\sqrt {x - m + 2} - 1}}\) với \(m\) là tham số. Tìm \(m\) để hàm số xác định trên \(\left( {0;1} \right)\)
ĐKXĐ \(\left\{ {\begin{array}{*{20}{c}}{x - m + 2 \ge 0}\\{\sqrt {x - m + 2} \ne 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge m - 2}\\{x \ne m - 1}\end{array}} \right.\)
Suy ra tập xác định của hàm số là ${\rm{D}} = \left[ {m - 2; + \infty } \right)\backslash \left\{ {m - 1} \right\}$.
Hàm số xác định trên \(\left( {0;1} \right) \Leftrightarrow \left( {0;1} \right) \subset \left[ {m - 2;m - 1} \right) \cup \left( {m - 1; + \infty } \right)\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left( {0;1} \right) \subset \left[ {m - 2;m - 1} \right)}\\{\left( {0;1} \right) \subset \left( {m - 1; + \infty } \right)}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2}\\{m - 1 \le 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2}\\{m \le 1}\end{array}} \right.\)
Vậy \(m \in \left( { - \infty ;1} \right] \cup \left\{ 2 \right\}\) là giá trị cần tìm.
Cho hàm số \(y = m{x^3} - 2({m^2} + 1){x^2} + 2{m^2} - m\). Tìm \(m\) để điểm \(M\left( { - 1;2} \right)\) thuộc đồ thị hàm số đã cho
Điểm \(M\left( { - 1;2} \right)\) thuộc đồ thị hàm số đã cho khi và chỉ khi
\(2 = - m - 2({m^2} + 1) + 2{m^2} - m \Leftrightarrow m = - 2\)
Vậy \(m = - 2\) là giá trị cần tìm.
Cho hàm số \(y = m{x^3} - 2({m^2} + 1){x^2} + 2{m^2} - m\). Tìm các điểm cố định mà đồ thị hàm số đã cho luôn đi qua với mọi \(m\).
Để \(N\left( {x;y} \right)\) là điểm cố định mà đồ thị hàm số đã cho luôn đi qua, điều kiện cần và đủ là \(y = m{x^3} - 2({m^2} + 1){x^2} + 2{m^2} - m,\,\,\forall m\)
\(\begin{array}{l} \Leftrightarrow 2{m^2}\left( {1 - {x^2}} \right) + m\left( {{x^3} - 1} \right) - 2{x^2} - y = 0,\,\,\,\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}1 - {x^2} = 0\\{x^3} - 1\\2{x^2} + y = 0\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = - 2}\end{array}} \right.\end{array}\)
Vậy đồ thị hàm số đã cho luôn đi qua điểm \(N\left( {1; - 2} \right)\).
Tịnh tiến đồ thị hàm số \(y = {x^2} + 1\) liên tiếp sang phải $2$ đơn vị và lên trên $1$ đơn vị ta được đồ thị của hàm số nào?
Ta tịnh tiến đồ thị hàm số \(y = {x^2} + 1\) sang phải $2$ đơn vị ta được đồ thị hàm số \(y = {\left( {x - 2} \right)^2}+1\) rồi tịnh tiến lên trên $1$ đơn vị ta được đồ thị hàm số \(y = {\left( {x - 2} \right)^2}+1+1\) hay \(y = {x^2} - 4x + 6\).
Vậy hàm số cần tìm là \(y = {x^2} - 4x + 6\).
Nêu cách tịnh tiến đồ thị hàm số \(y = - 2{x^2}\) để được đồ thị hàm số \(y = - 2{x^2} - 6x + 3\).
Ta có \( - 2{x^2} - 6x + 3 = - 2{\left( {x + \dfrac{3}{2}} \right)^2} + \dfrac{{15}}{2}\)
Do đó tịnh tiến đồ thị hàm số \(y = - 2{x^2}\) để được đồ thị hàm số \(y = - 2{x^2} - 6x + 3\) ta làm như sau
Tịnh tiến liên tiếp đồ thị hàm số \(y = - 2{x^2}\) đi sang bên trái \(\dfrac{3}{2}\) đơn vị và lên trên đi \(\dfrac{{15}}{2}\) đơn vị.
Nghiệm của phương trình \(\sqrt {2x - 7} = 1\) là
Điều kiện: \(x \ge \dfrac{7}{2}\) .
\(\sqrt {2x - 7} = 1\) \( \Rightarrow \) \(2x - 7 = 1 \Leftrightarrow x = 4\) .
Kết hợp với điều kiện ta được \(x = 4\) là nghiệm duy nhất..
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \( - {x^2} + x - m > 0\) vô nghiệm.
Bất phương trình \( - {x^2} + x - m > 0\) vô nghiệm khi và chỉ khi \( - {x^2} + x - m \le 0\), \(\forall x \in \mathbb{R}\).
Ta có \( - {x^2} + x - m \le 0\)\(\forall x \in \mathbb{R}\)\( \Leftrightarrow \Delta \le 0\) \( \Leftrightarrow 1 - 4m \le 0 \Leftrightarrow m \ge \dfrac{1}{4}\).
Tìm các giá trị thực của tham số \(m\) để phương trình \(\left( {m - 1} \right){x^2} - 2mx + m = 0\) có một nghiệm lớn hơn \(1\) và một nghiệm nhỏ hơn \(1\)?
Với \(m - 1 \ne 0\) ta xét phương trình: \(\left( {m - 1} \right){x^2} - 2mx + m = 0\)\(\left( 1 \right)\).
Ta có: \(\Delta ' = {b'^2} - ac\) \( = {m^2} - m\left( {m - 1} \right)\) \( = m\).
Để phương trình \(\left( 1 \right)\)có hai nghiệm phân biệt thì: \(\Delta ' > 0\) \( \Leftrightarrow m > 0\).
Giả sử \({x_1}\), \({x_2}\) là hai nghiệm của \(\left( 1 \right)\) và \({x_1} > 1\), \({x_2} < 1\).
Ta có: \(\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) < 0\)\( \Leftrightarrow \) \({x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 < 0\)\(\left( * \right)\).
Theo Vi-et ta có: \(\left\{ \begin{array}{l}{x_1}.{x_2} = \dfrac{m}{{m - 1}}\\{x_1} + {x_2} = \dfrac{{2m}}{{m - 1}}\end{array} \right.\), thay vào \(\left( * \right)\) ta có:
\(\dfrac{m}{{m - 1}} - \dfrac{{2m}}{{m - 1}} + 1 < 0\)\( \Leftrightarrow \) \(\dfrac{{ - 1}}{{m - 1}} < 0\)\( \Leftrightarrow m > 1\).
Vậy với \(m > 1\) thỏa mãn điều kiện bài toán.
Số nghiệm nguyên dương của phương trình \(\sqrt {x - 1} = x - 3\) là:
\(\sqrt {x - 1} = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right. \Leftrightarrow x = 5\).
Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) biết \(\left( P \right)\) đi qua \(A(2;3)\) có đỉnh \(I(1;2)\)
Vì \(A \in \left( P \right)\) nên \(3 = 4a + 2b + c\) (1).
Mặt khác \(\left( P \right)\) có đỉnh \(I(1;2)\) nên \( - \dfrac{b}{{2a}} = 1 \Leftrightarrow 2a + b = 0\) (2) và \(I \in \left( P \right)\) suy ra \(2 = a + b + c\) (3)
Từ (1), (2) và (3) ta có \(\left\{ \begin{array}{l}4a + 2b + c = 3\\2a + b = 0\\a + b + c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = 3\end{array} \right.\)
Vậy \(\left( P \right)\) cần tìm là $y = {x^2} - 2x + 3$.
Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) biết \(c = 2\) và \(\left( P \right)\) đi qua \(B\left( {3; - 4} \right)\) và có trục đối xứng là $x = - \dfrac{3}{2}$.
Ta có \(c = 2\) và \(\left( P \right)\) đi qua \(B\left( {3; - 4} \right)\) nên \( - 4 = 9a + 3b + 2 \Leftrightarrow 3a + b = - 2\) (*)
\(\left( P \right)\) có trục đối xứng là $x = - \dfrac{3}{2}$ nên \( - \dfrac{b}{{2a}} = - \dfrac{3}{2} \Leftrightarrow b = 3a\) thay vào (*) ta được \(3a + 3a = - 2 \Leftrightarrow a = - \dfrac{1}{3} \Rightarrow b = - 1\) .
Vậy \(\left( P \right)\) cần tìm là $y = - \dfrac{1}{3}{x^2} - x + 2$.
Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) biết hàm số có giá trị nhỏ nhất bằng \(\dfrac{3}{4}\) khi \(x = \dfrac{1}{2}\) và nhận giá trị bằng \(1\) khi $x = 1$.
Hàm số \(y = a{x^2} + bx + c\) có giá trị nhỏ nhất bằng \(\dfrac{3}{4}\) khi \(x = \dfrac{1}{2}\) nên ta có
\( - \dfrac{b}{{2a}} = \dfrac{1}{2} \Leftrightarrow a + b = 0\) (5)
\(\dfrac{3}{4} = a{\left( {\dfrac{1}{2}} \right)^2} + b\left( {\dfrac{1}{2}} \right) + c \) \(\Leftrightarrow a + 2b + 4c = 3\) (6) và $a > 0$
Hàm số \(y = a{x^2} + bx + c\) nhận giá trị bằng \(1\) khi $x = 1$ nên \(a + b + c = 1\)(7)
Từ (5), (6) và (7) ta có \(\left\{ \begin{array}{l}a + b = 0\\a + 2b + 4c = 3\\a + b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\\c = 1\end{array} \right.\)
Vậy phương trình \(\left( P \right)\) cần tìm là $y = {x^2} - x + 1$.
Tìm parabol $y = a{x^2} + 3x - 2$ , biết rằng parabol đó cắt trục $Ox$ tại điểm có hoành độ bằng $2$
Parabol cắt \(Ox\) tại điểm có hoành độ bằng \(2\) suy ra \(\left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\)
Ta có: \(0 = a{.2^2} + 3.2 - 2 \Leftrightarrow a = - 1\)
Vậy parabol \(y = - {x^2} + 3x - 2\)
Tính tổng các nghiệm của phương trình \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\)
ĐK: \(x \ge \dfrac{{ - 7}}{2}\)
Ta có \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 2} \right)\sqrt {2x + 7} = \left( {x - 2} \right)\left( {x + 2} \right)\\ \Leftrightarrow \left( {x - 2} \right)\left[ {\sqrt {2x + 7} - \left( {x + 2} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\sqrt {2x + 7} = x + 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}2x + 7 = {\left( {x + 2} \right)^2}\\x \ge - 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\2x + 7 = {x^2} + 4x + 4\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\{x^2} + 2x - 3 = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = 1\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Tổng hai nghiệm của phương trình là: \(2 + 1 = 3.\)
Cho hàm số \(y = {x^2} - 6x + 8\). Sử dụng đồ thị để tìm số điểm chung của đường thẳng \(y = m\left( { - 1 < m < 0} \right)\) và đồ thị hàm số trên.
Ta có \( - \dfrac{b}{{2a}} = 3,\,\, - \dfrac{\Delta }{{4a}} = - 1\)
Bảng biến thiên
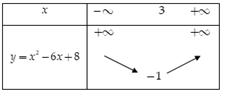
Suy ra đồ thị hàm số \(y = {x^2} - 6x + 8\) có đỉnh là \(I\left( {3; - 1} \right)\), đi qua các điểm \(A\left( {2;0} \right),\,\,B\left( {4;0} \right)\)
Nhận đường thẳng $x = 3$ làm trục đối xứng và hướng bề lõm lên trên.
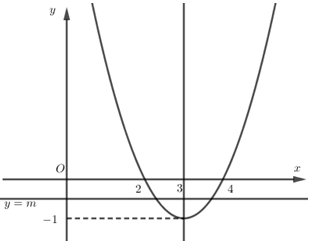
Đường thẳng \(y = m\left( { - 1 < m < 0} \right)\) song song với trục hoành nên ta thấy đường thẳng cắt đồ thị tại \(2\) điểm phân biệt.
Cho hàm số \(y = - {x^2} - 2x + 3\). Hãy tìm giá trị nhỏ nhất của hàm số đã cho trên \(\left[ { - 3;1} \right]\).
Ta có \( - \dfrac{b}{{2a}} = - 1,\,\, - \dfrac{\Delta }{{4a}} = 4\)
Bảng biến thiên
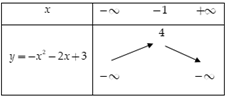
Suy ra đồ thị hàm số \(y = - {x^2} - 2x + 3\) có đỉnh là \(I\left( { - 1;4} \right)\), đi qua các điểm \(A\left( {1;0} \right),\,\,B\left( { - 3;0} \right)\)
Nhận đường thẳng $x = - 1$ làm trục đối xứng và hướng bề lõm xuống dưới.

Trên đoạn \(\left[ { - 3;1} \right]\)thì hàm số đạt GTNN \(y = 0\)
Cho phương trình ${x^2} + 2\left( {m + 3} \right)x + {m^2} - 3 = 0$, $m$ là tham số.
Tìm \(m\) để phương trình có hai nghiệm ${x_1},{x_2}$ và $P = 5({x_1} + {x_2}) - 2{x_1}{x_2}$ đạt giá trị lớn nhất.
Ta có \(\Delta ' = {\left( {m + 3} \right)^2} - \left( {{m^2} - 3} \right) = 6m + 12\)
Phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 6m + 12 \ge 0 \Leftrightarrow m \ge - 2\)
Theo định lý Viét ta có \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 2\left( {m + 3} \right)}\\{{x_1}{x_2} = {m^2} - 3}\end{array}} \right.\)
\(P = - 10\left( {m + 3} \right) - 2\left( {{m^2} - 3} \right) = - 2{m^2} - 10m - 24\)
Xét hàm số \(y = - 2{x^2} - 10x - 24\) với $x \in \left[ { - 2; + \infty } \right)$
Bảng biến thiên

Suy ra \(\mathop {max}\limits_{\left[ { - 2; + \infty } \right)} y = - 12\) khi và chỉ khi $x = - 2$
Vậy \(m = - 2\) là giá trị cần tìm.

