Cho mạnh điện như hình bên dưới. Biết \(U = 20\,\,V;\,\,R = 0,5\,\Omega ;\,\,{r_1} = 1\Omega ;\,\,{r_2} = 2\Omega \). Tìm cường độ dòng điện \({I_1},{I_2},\,I\) chạy qua mỗi điện trở.

D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
D. \(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cường độ dòng điện của đoạn mạch mắc song song là: \({I_1} + I\).
Ta có: \({I_2}\; = {I_1} + I\) hay \(I + {\rm{ }}{I_1}-{\rm{ }}{I_2}\; = 0\left( 1 \right).\)
Hiệu điện thế ở đoạn mạch mắc song song là: \(U' = {r_1}.{I_{1\;}} = R.I\) nên
\(1.{\rm{ }}{I_{1\;}} = 2.{\rm{ }}I\) hay \(2I-{I_1}\; = 0\left( 2 \right).\)
Hiệu điện thế của cả đoạn mạch là: \(U = {U_{2\;}} + U'\) nên:
\(20 = {r_2}.{\rm{ }}{I_2} + R.I\) hay \(2I + 0,5{I_2}\; = 20\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I + {I_1} - {I_2} = 0}\\{2I - {I_1} = 0}\\{2I + 0,5{I_2} = 20}\end{array}} \right.\)
Giải hệ phương trình, ta được:
\(I = \dfrac{{40}}{7}\left( A \right),\,{I_1} = \dfrac{{80}}{7}\left( A \right),\,{I_2} = \dfrac{{120}}{7}\left( A \right)\).
Cho sơ đồ mạch điện như sau. Biết rằng R = R1 = R2 = 5 Ω. Hãy tính các cường độ dòng điện I, I1 và I2.

A. \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
A. \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
A. \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
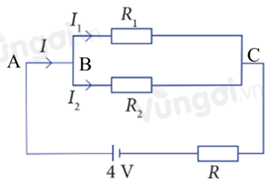
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau nên ta có I = I1 + I2 (1).
Hiệu điện thế giữa hai điểm A và C được tính bởi:
UAC = IR + I1R1 = 5I + 5I1 suy ra 5I + 5I1 = 4 (2).
Hiệu điện thế giữa hai điểm B và C được tính bởi:
UBC = I1R1 = I2R2 suy ra 5I1 = 5I2 hay I1 = I2 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I - {I_1} - {I_2} = 0,5}\\{5I + 5{I_1} = 4}\\{{I_1} - {I_2} = 0}\end{array}} \right.\)
Giải hệ này ta được \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
Cho mạch điện như hình sau. Biết U = 24 V, Ð1:12 V – 6 W, Ð2:12 V – 12 W, R = 3 Ω.

Điện trở của mỗi bóng đèn Đ1 và Đ2 là:
Điện trở của Đ1 là: R1 = \(\dfrac{{{{12}^2}}}{6}\)=24(Ω).
Điện trở của Đ2 là: R2 = \(\dfrac{{{{12}^2}}}{{12}}\)=12(Ω).
Cho mạch điện như hình sau. Biết U = 24 V, Ð1:12 V – 6 W, Ð2:12 V – 12 W, R = 3 Ω.

Cường độ dòng điện qua điện trở và các bóng đèn Đ1 , Đ2 là:
Gọi cường độ dòng điện qua điện trở R và các bóng đèn Đ1, Đ2 lần lượt là I, I1, I2 (ampe).
Cường độ dòng điện của đoạn mạch mắc song song là: I1 + I2.
Ta có: I = I1 + I2 hay I – I1 – I2 = 0 (1).
Hiệu điện thế ở đoạn mạch mắc song song là: U' = R1 . I1 = R2 . I2 nên
24 . I1 = 12 . I2 hay 2I1 – I2 = 0 (2).
Hiệu điện thế của đoạn mạch là: U = UR + U' nên
24 = R . I + R1 . I1 suy ra 3I + 24I1 = 24, hay I + 8I1 = 8 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I - {I_1} - {I_2} = 0}\\{2{I_1} - {I_2} = 0}\\{I + 8{I_1} = 8}\end{array}} \right.\)
Giải hệ phương trình, ta được:
\(I = \dfrac{{24}}{{11}}\left( A \right),\,{I_1} = \dfrac{8}{{11}}\left( A \right),\,{I_2} = \dfrac{{16}}{{11}}\left( A \right).\)
Tìm đa thức bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + 1\) (với a ≠ 0 ) biết \(f\left( {-1} \right) = \;-2,{\rm{ }}f\left( 1 \right) = 2,{\rm{ }}f\left( 2 \right) = 7.\)
A. \({x^3}-{x^2} + x + 1.\)
A. \({x^3}-{x^2} + x + 1.\)
A. \({x^3}-{x^2} + x + 1.\)
\(f\left( {-1} \right) =-2\; \Leftrightarrow a{\left( {-1} \right)^3}\; + {\rm{ }}b{\left( {-1} \right)^2}\; + {\rm{ }}c\left( {-1} \right) + 1 = -2\; \Leftrightarrow \;-a + b-c = -3{\rm{ }}\left( 1 \right)\)
\(f\left( 1 \right) = \;2 \Leftrightarrow \;a{.1^3}\; + b{.1^2}\; + c.1 + 1 = 2\; \Leftrightarrow a + b + c = 1{\rm{ }}\left( 2 \right)\)
\(\begin{array}{l}f\left( 2 \right) = \;7 \Leftrightarrow a{.2^3}\; + b{.2^2} + c.{\rm{ }}2 + 1 = 7\;\\ \Leftrightarrow \;8a + 4b + 2c = 6\\ \Leftrightarrow \;4a + 2b + c = 3{\rm{ }}\left( 3 \right)\end{array}\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{ - a + b - c = - 3}\\{a + b + c = 1}\\{4a + 2b + c = 3}\end{array}} \right.\)
Giải hệ này ta được a = 1, b = –1, c = 1.
Vậy đa thức f(x) là \({x^3}-{x^2} + x + 1.\)
Ba lớp 10A, 10B, 10C trồng được 164 cây bạch đàn và 316 cây thông. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 2 cây thông; mỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 3 cây thông; mỗi học sinh lớp 10C trồng được 5 cây thông. Biết số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C. Số học sinh của ba lớp 10A, 10B, 10C lần lượt là:
C. 32, 34, 30
C. 32, 34, 30
C. 32, 34, 30
Gọi số học sinh của ba lớp 10A, 10B, 10C lần lượt là x, y, z (học sinh) (x, y, z ∈ ℕ*).
Theo đề bài ta có:
- Số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C, suy ra:
\(x = \;\dfrac{{y + z}}{2} \Rightarrow 2x-y-z = 0{\rm{ }}\left( 1 \right).\)
- Số cây bạch đàn mỗi học sinh lớp 10A, 10B trồng được lần lượt là: 3, 2. Suy ra:
\(3x + 2y = 164{\rm{ }}\left( 2 \right).\)
- Số cây thông mỗi học sinh lớp 10A, 10B, 10C trồng được lần lượt là: 2, 3, 5. Suy ra:
\(2x + 3y + 5z\; = 316{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x - y - z = 0}\\{3x + 2y = 164}\\{2x + 3y + 5z = 316}\end{array}} \right.\)
Giải hệ này ta được x = 32, y = 34, z = 30 (thoả mãn điều kiện).
Vậy số học sinh của ba lớp 10A, 10B, 10C lần lượt là 32, 34, 30 học sinh.
Một giáo viên dạy Hoá tạo 1000 g dung dịch HCl 25% từ ba loại dung dịch HCl có nồng độ lần lượt là 10%, 20% và 30%. Biết rằng lượng HCl có trong dung dịch 10% bằng \(\dfrac{1}{4}\) lượng HCl có trong dung dịch 20%. Tính khối lượng dung dịch mỗi loại có nồng độ 10%, 20% và 30% .
B.125 g, 250 g, 625 g.
B.125 g, 250 g, 625 g.
B.125 g, 250 g, 625 g.
Gọi khối lượng dung dịch HCl có nồng độ 10%, 20% và 30% lần lượt là x, y, z (g).
Theo đề bài ta có: x + y + z = 1000 (1).
Vì dung dịch mới có nồng độ 25% nên ta có:
\(\dfrac{{10\% x + 20\% y + 30\% z}}{{1000}} = 25\% \)
\(\begin{array}{l} \Leftrightarrow 10x + 20y + 30z = 25\,\,000\\ \Leftrightarrow x + 2y + 3z = 2500\,\,(2)\end{array}\)
Lượng HCl có trong dung dịch 10% bằng lượng HCl có trong dung dịch 20%.
\( \Rightarrow 10\% x = \dfrac{1}{4}20\% y \Leftrightarrow 2x - y = 0\left( 3 \right)\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 1000}\\{x + 2y + 3z = 2500}\\{2x - y = 0}\end{array}} \right.\)
Giải hệ này ta được x = 125, y = 250, z = 625.
Vậy khối lượng dung dịch HCl có nồng độ 10%, 20% và 30% lần lượt là 125 g, 250 g, 625 g.
Một ngân hàng muốn đầu tư số tiền tín dụng là 100 tỉ đồng thu được vào ba nguồn: mua trái phiếu với mức sinh lời 8%/năm, cho vay thu lãi suất 10%/năm và đầu tư bất động sản với mức sinh lời 12%/năm. Theo điều kiện của quỹ tín dụng đề ra là tổng số tiền đầu tư vào trái phiếu và cho vay phải gấp ba lần số tiền đầu tư vào bất động sản. Ngân hàng muốn thu được mức thu nhập 9,6 tỉ đồng hằng năm, gọi số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là x, y, z (tỉ đồng).
Giá trị biểu thức: \(P = x + y - z\) là:
Giá trị biểu thức: \(P = x + y - z\) là:
Gọi số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là x, y, z (tỉ đồng).
Theo đề bài ta có: x + y + z = 100 (1).
Tổng số tiền đầu tư vào trái phiếu và cho vay gấp ba lần số tiền đầu tư vào bất động sản, do đó:
x + y = 3z hay x + y – 3z = 0 (2).
Lãi suất cho ba khoản đầu tư lần lượt là 8%, 10%, 12% và tổng số tiền lãi thu được là 9,6 tỉ đồng nên:
8%x + 10%y + 12%z = 9,6
suy ra 8x + 10y + 12z = 960 hay 4x + 5y + 6z = 480 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{x + y - 3z = 0}\\{4x + 5y + 6z = 480}\end{array}} \right.\)
Giải hệ này ta được x = 45, y = 30, z = 25.
Vậy số tiền đầu tư trái phiếu, cho vay, bất động sản lần lượt là 45 tỉ đồng, 30 tỉ đồng và 25 tỉ đồng.
=>\(P = 45 + 30 - 25 = 50\)
Độ cao h trong chuyển động của một vật được tính bởi công thức \(h = \;1212a{t^2} + {v_0}t + {h_0}\), với độ cao h và độ cao ban đầu h0 được tính bằng mét, t là thời gian của chuyển động tính bằng giây, a là gia tốc của chuyển động tính bằng m/s2, v0 là vận tốc ban đầu tính bằng m/s. Biết rằng sau 1s và 3s vật cùng đạt được độ cao 50,225 m; sau 2s vật đạt độ cao 55,125 m.
Tìm a, v0, h0
C.a = –9,8 m/s2; v0 = 19,6 m/s; h0 = 35,525 m
C.a = –9,8 m/s2; v0 = 19,6 m/s; h0 = 35,525 m
C.a = –9,8 m/s2; v0 = 19,6 m/s; h0 = 35,525 m
Theo đề bài ta có:
+ Với t = 1 thì h = 50,225
\( \Rightarrow 12a.12 + {v_0}.1 + {h_0} = 50,225 \Rightarrow 12a + {v_0} + {h_0} = 50,225\,\,\,\,\left( 1 \right).\)
+Với t = 3 thì h = 50,225
\( \Rightarrow 12a.32 + {v_0}.3 + {h_0} = 50,225 \Rightarrow 92a + 3{v_0} + {h_0} = 50,225\,\,\,\left( 2 \right).\)
+Với t = 2 thì h = 55,125
\( \Rightarrow 12a.22 + {v_0}.2 + {h_0} = 55,125 \Rightarrow 2a + 2{v_0} + {h_0} = 55,125\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{2}a + {v_0} + {h_0} = 50,225}\\{\dfrac{9}{2}a + 3{v_0} + {h_0} = 50,225}\\{2a + 2{v_0} + {h_0} = 55,125}\end{array}} \right.\)
Giải hệ này ta được a = –9,8; v0 = 19,6; h0 = 35,525.
Vậy a = –9,8 m/s2; v0 = 19,6 m/s; h0 = 35,525 m
Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích. Còn bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích. Biết giá tiền của bộ ba viên ngọc này là 270 triệu đồng. Chọn khẳng định đúng.
D. Ba viên bằng giá tiền nhau
D. Ba viên bằng giá tiền nhau
D. Ba viên bằng giá tiền nhau
Gọi giá tiền mỗi viên ngọc lam, hoàng ngọc, ngọc bích lần lượt là x, y, z \(\left( {x,y,z > 0} \right)\)(triệu đồng).
Theo đề bài ta có:
- Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích, suy ra:
$x + 2y = 3z$ hay $x + 2y –3z = 0 (1).$
- Bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích, suy ra:
$7x + y = 8z$ hay $7x + y – 8z = 0 (2).$
- Giá tiền của bộ ba viên ngọc là 270 triệu đồng, suy ra $x + y + z = 270 (3).$
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + 2y - 3z = 270}\\{7x + y - 8z = 0}\\{x + y + z = 270}\end{array}} \right.\)
Giải hệ này ta được $x = 90, y = 90, z = 90.$
Vậy giá tiền mỗi viên ngọc đều là 90 triệu đồng.
Cân bằng phương trình sau:
\(xKCl{O_3}\;\mathop \to \limits^{{t^o}} \;yKCl + z{O_2}\)
Giá trị biểu thức: \(A = x - 2y + z\) là:
Giá trị biểu thức: \(A = x - 2y + z\) là:
Theo định luật bảo toàn nguyên tố với K, Cl và O, ta có:
x = y hay x – y = 0 (1)
3x = 2z hay 3x – 2z = 0 (2)
Từ (1) và (2) ta có hệ phương trình:
Chọn z = 3. Khi đó hệ (1) trở thành.
\(\left\{ {\begin{array}{*{20}{c}}{x - y = 0}\\{3x - 2z = 0}\end{array}} \right.\)
Vậy ta có phương trình sau cân bằng: \(2KCl{O_3}\;\mathop \to \limits^{{t^o}} \;2KCl + 3{O_2}\)
=>\(A = 2 - 2.2 + 3 = 1\)
Bốn ngư dân góp vốn mua chung một chiếc thuyền. Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại. Người thứ hai đóng góp bằng \(\dfrac{1}{3}\) tổng số tiền của những người còn lại. Người thứ ba đóng góp bằng \(\dfrac{1}{4}\) tổng số tiền của những người còn lại. Người thứ tư đóng góp 130 triệu đồng.
Chiếc thuyền này được mua với giá
triệu đồng.
Chiếc thuyền này được mua với giá
triệu đồng.
Gọi số tiền người thứ nhất, người thứ hai, người thứ ba đóng góp lần lượt là x, y,z\(\left( {x,y,z > 0} \right)\) (triệu đồng).
Theo đề bài ta có:
- Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại, suy ra
\(x = \;\dfrac{1}{2}\left( {y + z + 130} \right)\) hay \(2x-y-z = 130{\rm{ }}\left( 1 \right).\)
- Người thứ hai đóng góp bằng \(\dfrac{1}{4}\) tổng số tiền của những người còn lại, suy ra:
\(y = \;1313\left( {x + z + 130} \right)\) hay \(-x + 3y-z = 130{\rm{ }}\left( 2 \right).\)
- Người thứ ba đóng góp bằng \(\dfrac{1}{4}\) tổng số tiền của những người còn lại, suy ra:
\(z = \;\dfrac{1}{4}\left( {x + y + 130} \right)\) hay \(-x-y + 4z = 130{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x - y - z = 130}\\{ - x + 3y - z = 130}\\{ - x - y + 4z = 130}\end{array}} \right.\)
Giải hệ này ta được \(x = 200,\,\,y = 150,\,\,z = 120\).
Suy ra tổng số tiền là: $200 + 150 + 120 + 130 = 600$ (triệu đồng).
Vậy chiếc thuyền này được mua giá 600 triệu đồng.
Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177. Trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 47. Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8.
Số hạt proton trong một nguyên tử A là:
Số hạt proton trong một nguyên tử A là:
Gọi ZA, NA lần lượt là số lượng hạt p, n của nguyên tử A.
ZB, NB lần lượt là số lượng hạt p, n của nguyên tử B.
Theo đề bài:
– Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177 nên ta có:
(2ZA + NA) + (2ZB + NB) = 177 (1).
– Số hạt mang điện nhiều hơn số hạt không mang điện là 47 nên ta có:
(2ZA + 2ZB) – (NA + NB) = 47 (2).
– Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8 nên ta có:
2ZB – 2ZA = 8 hay ZB – ZA = 4 (3).
Cộng theo từng vế của (1) với (2) ta được: 4ZA + 4ZB = 224 hay ZA + ZB = 56 (4).
Từ (3) và (4) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{{Z_B} - {Z_A} = 4}\\{{Z_A} + {Z_B} = 56}\end{array}} \right.\)
Giải hệ này ta được ZA = 26, ZB = 30.
Vậy số hạt proton trong một nguyên tử A là 26.
Một quỹ đầu tư dự kiến dành khoản tiền 1,2 tỉ đồng để đầu tư vào cồ phiếu. Để thấy được mức độ rủi ro, các cổ phiếu được phân thành ba loại: rủi ro cao, rủi ro trung bình và rủi ro thấp. Ban Giám đốc của quỹ ước tính các cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp sẽ có lợi nhuận hằng năm lần lượt là 15%, 10% và 6%. Nếu đặt ra mục tiêu đầu tư có lợi nhuận trung bình là 9%/năm trên tổng số vốn đầu tư, thì quỹ nên đầu tư bao nhiêu tiền vào mỗi loại cổ phiếu? Biết rằng, để an toàn, khoản đầu tư vào các cổ phiếu rủi ro thấp sẽ gấp đôi tổng các khoản đầu tư vào các cổ phiếu thuộc hai loại còn lại.
B.0,4 tỉ đồng, 0 đồng, 0,8 tỉ đồng.
B.0,4 tỉ đồng, 0 đồng, 0,8 tỉ đồng.
B.0,4 tỉ đồng, 0 đồng, 0,8 tỉ đồng.
Gọi số tiền nên đầu tư vào mỗi loại cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp lần lượt là x, y, z\(\left( {x,y,z > 0} \right)\) (tỉ đồng).
Theo đề bài ta có:
- Tổng số tiền đầu tư là 1,2 tỉ suy ra x + y + z = 1,2 (1).
- Mục tiêu đầu tư có lợi nhuận trung bình là 9%/năm trên tổng số vốn đầu tư, suy ra
$15%x + 10%y + 6%z = 9%.1,2$ hay $15x + 10y + 6z = 10,8$ (2).
- Khoản đầu tư vào các cổ phiếu rủi ro thấp sẽ gấp đôi tổng các khoản đầu tư vào các cổ phiếu thuộc hai loại còn lại, suy ra
$z=2(x + y)$ hay $2x+2y - z = 0$ (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 1,2}\\{15x + 10y + 6z = 10,8}\\{2x + 2y - z = 0}\end{array}} \right.\)
Giải hệ này ta được $x=0,4, y=0, z=0,8.$
Vậy số tiền nên đầu tư vào mỗi loại cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp lần lượt là 0,4 tỉ đồng, 0 đồng, 0,8 tỉ đồng.
Một đại lí bán ba mẫu máy điều hoà A, B và C, với giá bán mỗi chiếc theo từng mẫu lần lượt là 8 triệu đồng, 10 triệu đồng và 12 triệu đồng. Tháng trước, đại lí bán được 100 chiếc gồm cả ba mẫu và thu được số tiền là 980 triệu đồng. Tính số lượng máy điều hoà mỗi mẫu đại lí bán được trong tháng trước, biết rằng số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau.
A.30 chiếc, 50 chiếc, 20 chiếc.
A.30 chiếc, 50 chiếc, 20 chiếc.
A.30 chiếc, 50 chiếc, 20 chiếc.
Gọi số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Đại lí bán được 100 chiếc gồm cả ba mẫu, suy ra:
x + y + z = 100 (1).
- Số tiền thu được là 980 triệu đồng, suy ra:
8x + 10y + 12z = 980 hay 4x + 5y + 6z = 490 (2).
- Số tiền thu được từ bán máy điều hoà mẫu A và mẫu C là bằng nhau, suy ra
8x = 12z hay 2x –3z = 0 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 100}\\{4x + 5y + 6z = 490}\\{2x - 3z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 30, y = 50, z = 20.
Vậy số lượng máy điều hoà mỗi mẫu A, B, C đại lí bán được trong tháng trước lần lượt là 30, 50, 20.
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,5 và tổng số tế bào con tạo ra là 216. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại B được tạo ra ít hơn số tế bào con loại C được tạo ra là 40.
Số tế bào con mỗi loại A; B; C lúc ban đầu là:
;
;
Số tế bào con mỗi loại A; B; C lúc ban đầu là:
;
;
Gọi số tế bào con ban đầu mỗi loại A, B, C lần lượt là x, y, z.\(\left( {x,y,z \in {\mathbb{N}^*}} \right)\)
Theo đề bài ta có:
- Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,5.
Suy ra số tế bào con mỗi loại A, B, C lần lượt là:
\({2^3}x,{2^4}y,{2^5}z\) hay \(8x,16y,32z.\)
- Tổng số tế bào con tạo ra là 216, suy ra
$8x + 16y + 32z = 216$ hay $x + 2y + 4z = 27$ (1).
- Khi chưa thực hiện nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B, suy ra
$z = 1212(x + y)$ hay $x + y – 2z = 0$ (2).
- Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại B được tạo ra ít hơn số tế bào con loại C được tạo ra là 40, suy ra:
$8x + 16y = 32z – 40$ hay $x + 2y – 4z = –5$ (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + 2y + 4z = 27}\\{x + y - 2z = 0}\\{x + 2y - 4z = - 5}\end{array}} \right.\)
Giải hệ này ta được x = 5, y = 3, z = 4.
Vậy số tế bào con ban đầu mỗi loại A, B, C lần lượt là 5; 3; 4.
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra.
Số tế bào con loại A lúc ban đầu là:
Số tế bào con loại A lúc ban đầu là:
Gọi số tế bào con mỗi loại A, B, C lúc ban đầu lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,7.
Suy ra số tế bào con mỗi loại A, B, C được tạo ra lần lượt là:
\(2^3x, 2^4y\) và $ 2^7z$ hay $8x, 16y$ và $128z$
- Tổng số tế bào con tạo ra là 480, suy ra:
$ 8x + 16y + 128z = 480 (1).$
- Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C, suy ra:
$y = x + z hay x – y + z = 0 (2).$
– Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra, suy ra:
\(8x + 128z = 2.16y{\rm{ }} \Leftrightarrow 8x-32y + 128z = 0{\rm{ }}\\ \Leftrightarrow {\rm{ }}x-4y + 16z = 0{\rm{ }}\left( 3 \right).\)
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{8x + 16y + 127z = 480}\\{x - y + z = 0}\\{x - 4y + 16z = 0}\end{array}} \right.\)
Giải hệ này ta được x = 8, y = 10, z = 2.
Số tế bào con loại A lúc ban đầu là: 8
Cho A, B và C là ba dung dịch cùng loại acid có nồng độ khác nhau. Biết rằng nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M (mol/lít); nếu trộn 100 ml dung dịch A với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M; nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M. Mỗi dung dịch A, B và C có nồng độ bao nhiêu?
C.0,4 M; 0,7 M; 0,1 M.
C.0,4 M; 0,7 M; 0,1 M.
C.0,4 M; 0,7 M; 0,1 M.
Gọi nồng độ của mỗi dung dịch A, B, C lần lượt là x, y, z (M).
Theo đề bài ta có:
- Nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M, suy ra
\(\dfrac{{0,1x + 0,1y + 0,1z}}{{0,1 + 0,1 + 0,1}} = 0,4 \Leftrightarrow x + y + z = 1,2\) (1)
- Nếu trộn 100 ml dung dịch A với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M, suy ra
\(\dfrac{{0,1x + 0,2y}}{{0,1 + 0,2}} = 0,6 \Leftrightarrow x + 2y = 1,8\) (2)
- Nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M, suy ra
\(\dfrac{{0,1x + 0,2z}}{{0,1 + 0,2}} = 0,3 \Leftrightarrow y + 2y = 0,9\)(3)
Từ (1), (2) và (3) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + y + z = 1,2}\\{x + 2y = 1,8}\\{y + 2z = 0,9}\end{array}} \right.\)
Giải hệ này ta được $x = 0,4; y = 0,7; z =0,1.$
Vậy nồng độ của mỗi dung dịch A, B, C lần lượt là 0,4 M; 0,7 M; 0,1 M.
Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bảng sau.

Ngày hôm qua cửa hàng đã dùng hết 2 lít sữa đặc; 12,8 lít sữa tươi và 2,9 lít sữa chua.
Số li sinh tố xoài cửa hàng bán được trong ngày hôm qua là:
Số li sinh tố xoài cửa hàng bán được trong ngày hôm qua là:
Gọi số li sinh tố mỗi loại xoài, bơ, mãng cầu cửa hàng bán được trong ngày hôm qua lần lượt là x, y, z\((x,y,z \in {\mathbb{N}^*})\)
Theo đề bài ta có:
- Cửa hàng đã dùng hết 2 l hay 2000 ml sữa đặc, suy ra:
20x + 10y + 20z = 2000 hay 2x + y + 2z = 200 (1).
- Cửa hàng đã dùng hết 12,8 l hay 12800 ml sữa tươi, suy ra:
100x + 120y + 100z = 12800 hay 5x + 6y + 5z = 640 (2).
- Cửa hàng đã dùng hết 2,9 l hay 2900 ml sữa chua, suy ra:
30x + 20y + 20z = 2900 hay 3x + 2y + 2z = 290 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{2x + y + 2z = 200}\\{5x + 6y + 5z = 640}\\{3x + 2y + 2z = 290}\end{array}} \right.\)
Giải hệ này ta được x = 50, y = 40, z = 30.
Vậy số li sinh tố xoài cửa hàng bán được trong ngày hôm qua là 50.
Xăng sinh học E5 là hỗn hợp xăng không chì truyền thống và cồn sinh học (bio – ethanol). Trong loại xăng này chứa 5% cồn sinh học. Khi động cơ đốt cháy lượng cồn trên thì xảy ra phản ứng hoá học
\(x{C_2}{H_6}O{\rm{ }} + {\rm{ y}}{O_2}\;\mathop \to \limits^{{t^o}} zC{O_2}\; + {\rm{ t}}{H_2}O.\)
Cân bằng phương trình hoá học trên để phương trình có hệ số đơn giản, ta được tổng \(x + y + z + t = \)
Cân bằng phương trình hoá học trên để phương trình có hệ số đơn giản, ta được tổng \(x + y + z + t = \)
\(x{C_2}{H_6}O{\rm{ }} + {\rm{ y}}{O_2}\;\mathop \to \limits^{{t^o}} zC{O_2}\; + {\rm{ t}}{H_2}O.\)
Số nguyên tử C ở hai vế bằng nhau, ta có 2x = z (1).
Số nguyên từ H ở hai vế bằng nhau, ta có 6x = 2t hay 3x = t (2).
Số nguyên từ O ở hai vế bằng nhau, ta có x + 2y = 2z + t (3).
Thay (1) và (2) vào (3) ta được x + 2y = 2 . 2x + 3x hay y = 3x.
Vậy y = 3x, z = 2x, t = 3x.
Để phương trình có hệ số đơn giản, ta chọn x = 1, khi đó y = 3, z = 2, t = 3.
\( \Rightarrow \,x + y + z + t = 1 + 2 + 3 + 2 = 8\)

