Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là
Miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là miền trong của tam giác $ABC$ kể cả biên (như hình)

Ta thấy \(F = y - x\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A\), \(B\), \(C\).
Tại \(A\left( {0; 2} \right)\) thì \(F = 2\).
Tại \(B\left( {1; 4} \right)\) thì \(F = 3\)
Tại \(A\left( {2; 3} \right)\) thì \(F = 1\).
Vậy \(\min F = 1\) khi \(x = 2\), \(y = 3\).
Một gia đình cần ít nhất \(900\) đơn vị protein và \(400\) đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa \(800\) đơn vị protein và \(200\)đơn vị lipit. Mỗi kilogam thịt lợn chứa \(600\) đơn vị protein và \(400\) đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất \(1,6\) kg thịt bò và \(1,1\) kg thịt lợn. Giá tiền một kg thịt bò là \(160\) nghìn đồng, một kg thịt lợn là \(110\) nghìn đồng. Gọi \(\,x\),\(y\) lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm \(\,x\),\(y\) để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?
Theo bài ra ta có số tiền gia đình cần trả là \(160.x + 110.y\) với \(\,x\),\(y\) thỏa mãn: \(\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\end{array} \right.\).
Số đơn vị protein gia đình có là \(0,8.x + 0,6.y \ge 0,9\)\( \Leftrightarrow 8x + 6y \ge 9\)\(\left( {{d_1}} \right)\).
Số đơn vị lipit gia đình có là\(0,2.x + 0,4.y \ge 0,4 \Leftrightarrow \,x + 2y \ge 2\) \(\left( {{d_2}} \right)\).
Bài toán trở thành: Tìm \(x,y\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.\) sao cho \(T = 160.x + 110.y\) nhỏ nhất.

Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm \(A\left( {1,6;\,1,1} \right)\); \(B\left( {1,6;\,0,2} \right)\); \(C\left( {0,6;\,0,7} \right)\); \(D\left( {0,3;\,1,1} \right)\).
Nhận xét: \(T\left( A \right) = 377\) nghìn, \(T\left( B \right) = 278\) nghìn, \(T\left( C \right) = 173\) nghìn, \(T\left( D \right) = 169\) nghìn.
Ta thấy, T(D) nhỏ nhất nên x=0,3, y=1,1.
Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì \(x = 0,3\) và \(y = 1,1\).
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm \(I\) và \(II\). Mỗi sản phẩm \(I\) bán lãi \(500\) nghìn đồng, mỗi sản phẩm \(II\) bán lãi \(400\) nghìn đồng. Để sản xuất được một sản phẩm \(I\) thì Chiến phải làm việc trong \(3\) giờ, Bình phải làm việc trong \(1\) giờ. Để sản xuất được một sản phẩm \(II\) thì Chiến phải làm việc trong \(2\) giờ, Bình phải làm việc trong \(6\) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá \(180\) giờ và Bình không thể làm việc quá \(220\) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.
Gọi \(x\), \(y\) lần lượt là số sản phẩm loại \(I\) và loại \(II\) được sản xuất ra. Điều kiện \(x\), \(y\) nguyên dương.
Ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x + 2y \le 180\\x + 6y \le 220\\x > 0\\y > 0\end{array} \right.\)
Miền nghiệm của hệ trên là
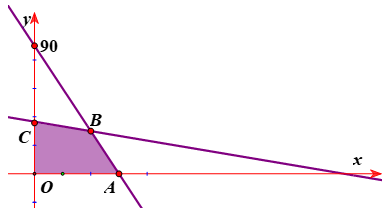
Tiền lãi trong một tháng của xưởng là \(T = 0,5x + 0,4y\) (triệu đồng).
Ta thấy \(T\) đạt giá trị lớn nhất chỉ có thể tại các điểm \(A\), \(B\), \(C\). Vì \(C\) có tọa độ không nguyên nên loại.
Tại \(A\left( {60; 0} \right)\) thì \(T = 30\) triệu đồng.
Tại \(B\left( {40; 30} \right)\) thì \(T = 32\) triệu đồng.
Vậy tiền lãi lớn nhất trong một tháng của xưởng là \(32\) triệu đồng.
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.
Bước 1:
Số tiền bán x vé loại 1 là: \(x.50000\) (đồng)
Số tiền bán y vé loại 2 là: \(y.100000\) (đồng)
Bước 2:
Số tiền thu được là
\(50000x + 100000y\) (đồng)
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Các số nguyên không âm x và y phải thoả mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50000x + 100000y \ge {2.10^7}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50000x + 100000y < {2.10^7}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Điều kiện xác định: \(x \ge 0.\)
\(\left\{ \begin{array}{l}3x - 5 + \sqrt x < 2x + \sqrt x \\2{x^2} - 5x + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 5\\\left( {x - 1} \right)\left( {2x - 3} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 5\\\left[ \begin{array}{l}x > \dfrac{3}{2}\\x < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\dfrac{3}{2} < x < 5\\x < 1\end{array} \right..\)
Kết hợp với điều kiện \(x \ge 0\) ta được tập nghiệm của hệ bất phương trình đã cho là: \(S = \left[ {0;\,1} \right) \cup \left( {\dfrac{3}{2};\,\,5} \right).\)
Một gian hàng trưng bày bàn và ghế rộng 60 \({m^2}\). Diện tích để kê một chiếc ghế là 0,5\({m^2}\), một chiếc bàn là 1,2 \({m^2}\). Gọi x là số chiếc ghế, y là số chiếc bàn được kê.
Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12 \({m^2}\).
Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.
Diện tích của x chiếc ghế là \(0,5x\left( {{m^2}} \right)\) và y chiếc bàn là \(1,2y\left( {{m^2}} \right)\)
Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng 12 \({m^2}\).
Tổng diện tích x chiếc ghế và y chiếc bàn là \(0,5x + 1,2y\left( {{m^2}} \right)\)
Diện tích lưu thông là \(60 - 0,5x - 1,2y\left( {{m^2}} \right)\)
Bất phương trình cần tìm là
\(\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}\)
Một gian hàng trưng bày bàn và ghế rộng 60 \({m^2}\). Diện tích để kê một chiếc ghế là 0,5\({m^2}\), một chiếc bàn là 1,2 \({m^2}\). Gọi x là số chiếc ghế, y là số chiếc bàn được kê.
Trong các cặp số (10;10), (10;20) và (20;10), có bao nhiêu cặp là nghiệm của bất phương đã lập được?
+) Thay x=10, y=10 ta được
=> (10;10) là nghiệm của bất phương trình
+) Thay x=10, y=20 ta được
=> (10;20) là nghiệm của bất phương trình
+) Thay x=20, y=10 ta được
=> (20;10) là nghiệm của bất phương trình.
Vậy cả 3 cặp số là nghiệm của bất phương trình.
Cho hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x - y < 3\left( 1 \right)\\x + 2y > - 2\left( 2 \right)\end{array} \right.\)
Cặp số là nghiệm của bất phương trình đã cho là:
(1;1)
(1;1)
(1;1)
+ Thay x=1;y=1 vào (1) ta được: 1-1<3(Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2(Luôn đúng)
Vậy cặp số (1;1) là nghiệm của hệ bất phương trình đã cho.
+ Thay x=-5;y=1 vào (1) ta được: -5-1<3(Luôn đúng)
Thay x=-5; y=1 vào (2) ta được: -5+2.1>-2(Sai)
Vậy cặp số (-5;1) là không nghiệm của hệ bất phương trình đã cho.
Miền không bị gạch ở hình sau là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
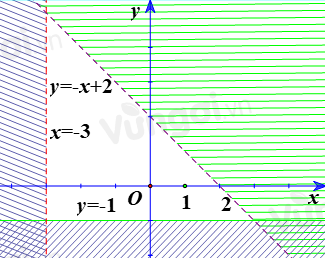
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = 2\)
Từ các phương trình trên thì ta chọn luôn hệ thứ nhất mà không cần xét tiếp.

