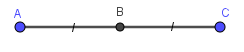
Cho tam giác \(ABC\). Gọi M, N, P lần lượt là trung điểm của \(BC,\,\,CA,\,\,AB\), \(O\) là điểm bất kì. Khẳng định nào sau đây là đúng nhất?

Theo quy tắc ba điểm ta có
\(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OP} + \overrightarrow {PA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) + \overrightarrow {PA} + \overrightarrow {MB} + \overrightarrow {NC} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) - \left( {\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} } \right)\end{array}\)
Vì \(PN,\,MN\) là đường trung bình của tam giác \(ABC\) nên
\(PN//BM,\,\,MN//BP\) suy ra tứ giác \(BMNP\) là hình bình hành
\( \Rightarrow \overrightarrow {BM} = \overrightarrow {PN} \)
\(N\) là trung điểm của \(AC \Rightarrow \overrightarrow {CN} = \overrightarrow {NA} \)
Do đó theo quy tắc ba điểm ta có
\(\begin{array}{l}\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \left( {\overrightarrow {PN} + \overrightarrow {NA} } \right) + \overrightarrow {AP} \\ = \overrightarrow {PA} + \overrightarrow {AP} = \overrightarrow 0 \end{array}\)
Do đó \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \)
Đơn giản biểu thức \(C = \dfrac{1}{{\sin 10^\circ }} + \dfrac{{\sqrt 3 }}{{\cos 10^\circ }}\).
\(C = \dfrac{1}{{\sin {{10}^o}}} + \dfrac{{\sqrt 3 }}{{\cos {{10}^o}}} = \dfrac{{\cos {{10}^{\rm{o}}} + \sqrt 3 \sin {{10}^{\rm{o}}}}}{{\sin {{10}^{\rm{o}}}\cos {{10}^{\rm{o}}}}} = \dfrac{{\dfrac{1}{2}\cos {{10}^{\rm{o}}} + \dfrac{{\sqrt 3 }}{2}\sin {{10}^{\rm{o}}}}}{{\dfrac{{2\sin {{10}^{\rm{o}}}\cos {{10}^{\rm{o}}}}}{4}}} = \dfrac{{4\sin {{40}^{\rm{o}}}}}{{\sin {{20}^{\rm{o}}}}} = 8\cos {20^{\rm{o}}}\).
Cho tứ giác ABCD có \(\overrightarrow {AD} = \overrightarrow {BC} \). Mệnh đề nào trong các mệnh đề sau là sai?

Dựa vào hình vẽ ta thấy ABCD là hình bình hành nên A đúng.
\( \Rightarrow AD = BC \Rightarrow \) B đúng.
Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng và AB = DC nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow D\) đúng.
Vậy C sai. (2 đường chéo của hình bình hành không bằng nhau)
Cho $\tan \alpha + \cot \alpha = m$. Tính giá trị biểu thức ${\tan ^3}\alpha + {\cot ^3}\alpha $.
${\tan ^3}\alpha + {\cot ^3}\alpha = {\left( {\tan \alpha + \cot \alpha } \right)^3} - 3\tan \alpha .\cot \alpha \left( {\tan \alpha + \cot \alpha } \right) = {m^3} - 3m$.
Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là:
Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương
\( \Leftrightarrow \exists k \ne 0:\overrightarrow {AB} = k\overrightarrow {AC} \).
Giá trị của $\tan {180^0}$ bằng:
Ta có: \(\tan {180^0} = 0\)
Cho hình thoi \(ABCD\) cạnh $a$ và \(\widehat {BCD} = {60^0}\). Gọi $O$ là tâm hình thoi. Chọn kết luận đúng:
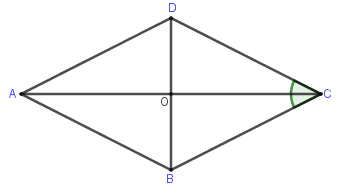
Ta có \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\) (quy tắc hình bình hành)
Xét tam giác \(BCD\) có \(CD = CB = a\) và góc \(\widehat {BCD} = {60^0}\) nên tam giác \(BCD\) đều cạnh \(a\)
Xét tam giác \(DOC\) có \(\widehat O = {90^0}\) và \(DC = a,DO = \dfrac{1}{2}DB = \dfrac{a}{2}\) nên \(CO = \sqrt {D{C^2} - D{O^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
Do đó \(AC = 2OC = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \) hay \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 3 \) nên A đúng.
Lại có:
\(\overrightarrow {OB} - \overrightarrow {DC} = \overrightarrow {DO} - \overrightarrow {DC} = \overrightarrow {CO} \) nên \(\left| {\overrightarrow {OB} - \overrightarrow {DC} } \right| = \left| {\overrightarrow {CO} } \right| = CO = \dfrac{{a\sqrt 3 }}{2}\)
\(\left| {\overrightarrow {OB} - \overrightarrow {DC} } \right| = \left| {\overrightarrow {CO} } \right| = \,\,\dfrac{{a\sqrt 3 }}{2} \ne \dfrac{{a\sqrt 3 }}{4}\) nên B sai.
Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). \(M\) là một điểm bất kỳ. Chứng minh rằng \(\overrightarrow u = \overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} - \overrightarrow {MD} \) không phụ thuộc vị trí điểm \(M\). Tính độ dài vectơ \(\overrightarrow u \)
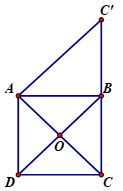
Theo quy tắc phép trừ ta có
\(\overrightarrow u = \left( {\overrightarrow {MA} - \overrightarrow {MC} } \right) + \left( {\overrightarrow {MB} - \overrightarrow {MD} } \right) = \overrightarrow {CA} + \overrightarrow {DB} \)
Suy ra \(\overrightarrow u \) không phụ thuộc vị trí điểm \(M\).
Qua \(A\) kẻ đường thẳng song song với \(DB\) cắt \(BC\) tại \(C'\).
Khi đó tứ giác \(ADBC'\) là hình bình hành (vì có cặp cạnh đối song song) suy ra \(\overrightarrow {DB} = \overrightarrow {AC'} \)
Do đó \(\overrightarrow u = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \)
=> \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {CC'} } \right| =CC'= BC + BC' \)
Mà ta có $BC'=AD=a$ (do $ADBC'$ là hình bình hành) và $BC=a$ (gt)
Vậy \(\left| {\overrightarrow u } \right| = a + a = 2a\)
Cho hai tam giác ABC và A’B’C’ lần lượt có trọng tâm G và G’. Đẳng thức nào dưới đây là sai?
Vì G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên ta có:
\(\begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} = \overrightarrow 0 .\end{array}\)
Với điểm M bất kì khác điểm G ta chứng minh: \(3\overrightarrow {MG} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \)
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \) \(= \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG} \)
Tương tự ta có: \(3\overrightarrow {MG'} = \overrightarrow {MA'} + \overrightarrow {MB'} + \overrightarrow {MC'} \)
Từ đó suy ra
\(\begin{array}{l}3\overrightarrow {GG'} = 3\left( {\overrightarrow {MG'} - \overrightarrow {MG} } \right) = 3\overrightarrow {MG'} - 3\overrightarrow {MG} \\ = \overrightarrow {MA'} + \overrightarrow {MB'} + \overrightarrow {MC'} - \overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} \\ = \left( {\overrightarrow {MA'} - \overrightarrow {MA} } \right) + \left( {\overrightarrow {MB'} - \overrightarrow {MB} } \right) + \left( {\overrightarrow {MC'} - \overrightarrow {MC} } \right)\\ = \overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} .\end{array}\)
Nên A đúng.
Đáp án B:
\(\begin{array}{l}3\overrightarrow {GG'} = \overrightarrow {GG'} + \overrightarrow {GG'} + \overrightarrow {GG'} \\ = \overrightarrow {GA} + \overrightarrow {AC'} + \overrightarrow {C'G'} + \overrightarrow {GB} + \overrightarrow {BA'} + \overrightarrow {A'G'} \\ + \overrightarrow {GC} + \overrightarrow {CB'} + \overrightarrow {B'G'} \\ = \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} } \right)\\ + \left( {\overrightarrow {C'G'} + \overrightarrow {A'G'} + \overrightarrow {B'G'} } \right)\\ = \overrightarrow 0 + \left( {\overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} } \right) + \overrightarrow 0 \\ = \overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} \end{array}\)
Nên B đúng.
Đáp án C:
\(\begin{array}{l}3\overrightarrow {GG'} = \overrightarrow {GG'} + \overrightarrow {GG'} + \overrightarrow {GG'} \\ = \overrightarrow {GA} + \overrightarrow {AB'} + \overrightarrow {B'G'} + \overrightarrow {GB} + \overrightarrow {BC'} + \overrightarrow {C'G'} \\ + \overrightarrow {GC} + \overrightarrow {CA'} + \overrightarrow {A'G'} \\ = \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} } \right)\\ + \left( {\overrightarrow {B'G'} + \overrightarrow {C'G'} + \overrightarrow {A'G'} } \right)\\ = \overrightarrow 0 + \left( {\overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} } \right) + \overrightarrow 0 \\ = \overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} \end{array}\)
Nên C đúng.
D sai do A đúng.
Cho tam giác \(ABC\) vuông tại \(A\) có và \(BC = a\sqrt 5 \). Tính độ dài của vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).

Gọi \(D\) là điểm sao cho tứ giác \(ABDC\) là hình bình hành.
Khi đó theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Vì tam giác \(ABC\) vuông ở \(A\) nên tứ giác \(ABDC\) là hình chữ nhật suy ra \(AD = BC = a\sqrt 5 \)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 5 \)
Cho hình bình hành \(ABCD\). Trên các đoạn thẳng\(DC,\,\,AB\) theo thứ tự lấy các điểm \(M,\,\,N\) sao cho \(DM = BN\). Gọi \(P\) là giao điểm của \(AM,\,\,DB\) và \(Q\) là giao điểm của \(CN,\,\,DB\). Khẳng định nào sau đây là đúng?
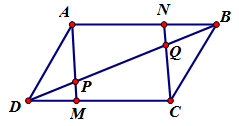
Ta có \(DM = BN \Rightarrow AN = MC\), mặt khác \(AN\) song song với \(MC\) do đó tứ giác \(ANCM\) là hình bình hành
Suy ra \(\overrightarrow {AM} = \overrightarrow {NC} \).
Xét tam giác \(\Delta DMP\) và \(\Delta BNQ\) ta có \(DM = NB\) (giả thiết), \(\widehat {PDM} = \widehat {QBN}\) (so le trong)
Mặt khác \(\widehat {DMP} = \widehat {APB}\) (đối đỉnh) và \(\widehat {APQ} = \widehat {NQB}\) (hai góc đồng vị) suy ra \(\widehat {DMP} = \widehat {BNQ}\).
Do đó \(\Delta DMP = \Delta BNQ\) (c.g.c) suy ra \(DP = QB\).
Dễ thấy \(\overrightarrow {DP} ,\,\,\overrightarrow {QB} \) cùng hướng vì vậy \(\overrightarrow {DP} = \overrightarrow {QB} \).
Cho tam giác \(ABC\) có trọng tâm \(G\). Gọi \(I\) là trung điểm của \(BC\). Dựng điểm \(B'\) sao cho \(\overrightarrow {B'B} = \overrightarrow {AG} \), gọi $J$ là trung điểm của \(BB'\). Khẳng định nào sau đây là đúng?

Ta có \(\overrightarrow {B'B} = \overrightarrow {AG} \) suy ra \(B'B = AG\).
Dễ thấy \(\overrightarrow {BJ} ,\,\,\overrightarrow {IG} \) cùng hướng (1).
Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(IG = \dfrac{1}{2}AG\), \(J\) là trung điểm \(BB'\) suy ra \(BJ = \dfrac{1}{2}BB'\)
Vì vậy \(BJ = IG\) (2)
Từ (1) và (2) ta có \(\overrightarrow {BJ} = \overrightarrow {IG} \).
Cho tam giác ABC và I thỏa mãn \(\overrightarrow {IA} = 3\overrightarrow {IB} \). Đẳng thức nào sau đây là đẳng thức đúng.
Ta có:
\(\begin{array}{l}\overrightarrow {CI} = \overrightarrow {CA} - \overrightarrow {IA} = \overrightarrow {CA} - 3\overrightarrow {IB} = \overrightarrow {CA} - 3\left( {\overrightarrow {CB} - \overrightarrow {CI} } \right)\\ \Leftrightarrow \overrightarrow {CI} = \overrightarrow {CA} - 3\overrightarrow {CB} + 3\overrightarrow {CI} \\ \Leftrightarrow 2\overrightarrow {CI} = 3\overrightarrow {CB} - \overrightarrow {CA} \\ \Leftrightarrow \overrightarrow {CI} = \dfrac{1}{2}\left( {3\overrightarrow {CB} - \overrightarrow {CA} } \right)\end{array}\)
Cho tam giác $ABC$ đều cạnh bằng $1$. Tính \(\overrightarrow {AB} .\overrightarrow {BC} \) ?
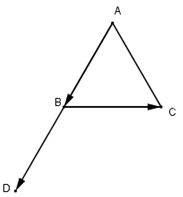
Lấy điểm $D$ sao cho \(\overrightarrow {AB} = \overrightarrow {BD} \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BD} ;\overrightarrow {BC} } \right) = {120^0}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 1.1.\cos {120^0} = - \dfrac{1}{2}\)
(vì tam giác $ABC$ đều cạnh $1$ nên \(AB = BC = 1 \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = 1\))
Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\); \(I\) là trung điểm của \(AD\) . Khi đó \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \) bằng:

Ta có \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} = \left( {\overrightarrow {IA} + \overrightarrow {IA} + \overrightarrow {AB} } \right).\overrightarrow {ID} = 2\overrightarrow {IA} .\overrightarrow {ID} = - \dfrac{{9{a^2}}}{2}\) nên chọn B.
Nếu $\sin x = \dfrac{4}{5}$ thì giá trị của $\cos 4x = ?$
$\cos 4x = 2{\cos ^2}2x - 1$ $ = 2.{\left( {1 - 2{{\sin }^2}x} \right)^2} - 1$ $ = 2{\left( {1 - 2.{{\left( {\dfrac{4}{5}} \right)}^2}} \right)^2} - 1$ $ = - \dfrac{{527}}{{625}}$
Cho tam giác \(ABC\) đều cạnh \(a\) và \(G\) là trọng tâm. Gọi \(I\) là trung điểm của \(AG\). Tính độ dài của vectơ $\overrightarrow {BI} $.

Ta có $\left| {\overrightarrow {AB} } \right| = AB = a$
Gọi $M$ là trung điểm của \(BC\)\( \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{a}{2}\)
Tam giác \(ABM\) vuông tại \(M\) nên \(AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
Ta có \(\left| {\overrightarrow {AG} } \right| = AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Mà \(I\) là trung điểm của \(AG\) nên \(MI = AG = \dfrac{{a\sqrt 3 }}{3}\)
\(\left| {\overrightarrow {BI} } \right| = BI = \sqrt {B{M^2} + M{I^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt {21} }}{6}\)
Nếu $\sin a - \cos a = \dfrac{1}{5}\,\,\left( {{{135}^0} < a < {{180}^0}} \right)$ thì giá trị đúng của $\tan 2a$ là:
$\sin a - \cos a = \dfrac{1}{5}\, \Rightarrow {\left( {\sin a - \cos a} \right)^2} = \dfrac{1}{{25}} \Leftrightarrow {\sin ^2}a - 2\sin a\cos a + {\cos ^2}a = \dfrac{1}{{25}} \Leftrightarrow 1 - \sin 2a = \dfrac{1}{{25}} \Leftrightarrow \sin 2a = \dfrac{{24}}{{25}}$
Ta có: ${\sin ^2}2a + {\cos ^2}2a = 1 \Rightarrow {\left( {\dfrac{{24}}{{25}}} \right)^2} + {\cos ^2}2a = 1 \Leftrightarrow {\cos ^2}2a = \dfrac{{49}}{{625}} \Leftrightarrow \cos 2a = \pm \dfrac{7}{{25}}$
Mà ${135^0} < a < {180^0} \Leftrightarrow {270^0} < 2a < {360^0} \Rightarrow \cos 2a > 0 \Rightarrow \cos 2a = \dfrac{7}{{25}}$
$\tan 2a = \dfrac{{\sin 2a}}{{\cos 2a}} = \dfrac{{\dfrac{{24}}{{25}}}}{{\dfrac{7}{{25}}}} = \dfrac{{24}}{7}$
Cho hình thoi \(ABCD\) có tâm \(O\). Hãy cho biết số khẳng định đúng ?
a) \(\overrightarrow {AB} = \overrightarrow {BC} \)
b) \(\overrightarrow {AB} = \overrightarrow {DC} \)
c) \(\overrightarrow {OA} = - \overrightarrow {OC} \)
d) \(\overrightarrow {OB} = \overrightarrow {OA} \)
e) \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)
f) \(2\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {BD} } \right|\)
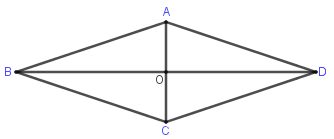
a) Sai vì hai véc tơ \(\overrightarrow {AB} ,\overrightarrow {BC} \) không cùng hướng.
b) Đúng vì hai véc tơ \(\overrightarrow {AB} ,\overrightarrow {DC} \) cùng hướng và cùng độ dài.
c) Đúng vì hai véc tơ \(\overrightarrow {OA} \) và \(\overrightarrow {OC} \) đối nhau.
d) Sai vì \(\overrightarrow {OA} ,\overrightarrow {OB} \) không cùng độ dài và không cùng hướng
e) Đúng vì \(AB = BC\)
f) Sai vì \(2\left| {\overrightarrow {OA} } \right| = 2OA = AC \ne BD = \left| {\overrightarrow {BD} } \right|\)
Vậy có \(3\) khẳng định đúng.
Cho \(3\) điểm phân biệt \(A,B,C\). Nếu \(\overrightarrow {AB} = \overrightarrow {BC} \) thì có nhận xét gì về ba điểm $A,B,C$?
Vì \(\overrightarrow {AB} = \overrightarrow {BC} \) nên \(\overrightarrow {AB} ,\overrightarrow {BC} \) cùng hướng và \(AB = BC\) nên \(B\) là trung điểm của \(AC\)