Cho $\sin a = \dfrac{3}{5}$ và ${90^0} < a < {180^0}$. Tính $A = \dfrac{{\cot a - 2\tan a}}{{\tan \,a + 3\cot a}}$.
$A = \dfrac{{\cot a - 2\tan a}}{{\tan \,a + 3\cot a}} = \dfrac{{\cot \,a - \dfrac{2}{{\cot a}}}}{{\dfrac{1}{{\cot a}} + 3\cot a}} = \dfrac{{{{\cot }^2}a - 2}}{{1 + 3{{\cot }^2}a}}$
Mà: ${\cot ^2}a + 1 = \dfrac{1}{{{{\sin }^2}a}} \Leftrightarrow {\cot ^2}a + 1 = \dfrac{1}{{{{\left( {\dfrac{3}{5}} \right)}^2}}} \Leftrightarrow {\cot ^2}a = \dfrac{{16}}{9}$
$ \Rightarrow A = \dfrac{{\dfrac{{16}}{9} - 2}}{{1 + 3.\dfrac{{16}}{9}}} = - \dfrac{2}{{57}}$
Cho hình vuông ABCD cạnh a, tâm O. Gọi M là điểm tùy ý trên đường tròn nội tiếp hình vuông. Tính $\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} $.
Ta có
$\begin{array}{l}\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OD} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2M{O^2} + \overrightarrow {OA} .\overrightarrow {OB} + \overrightarrow {OC.} \overrightarrow {OD} + \overrightarrow {MO} \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right).\end{array}$
Có \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ;\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\(\overrightarrow {OA} \bot \overrightarrow {OB} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0,\overrightarrow {OC} \bot \overrightarrow {OD} \Rightarrow \overrightarrow {OC} .\overrightarrow {OD} = 0\)
Đường tròn nội tiếp hình vuông cạnh a có bán kính \(\dfrac{a}{2} \Rightarrow MO = \dfrac{a}{2} \Rightarrow M{O^2} = \dfrac{{{a^2}}}{4}.\)
Vậy $\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} = 2.\dfrac{{{a^2}}}{4} = \dfrac{{{a^2}}}{2}$
Cho tam giác ABC vuông cân tại A. Tính cos góc giữa hai trung tuyến BE,CF.
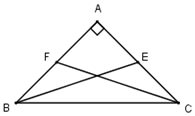
Gọi a là góc tạo bởi hai trung tuyến BE,CF.
Khi đó $\cos a = \dfrac{{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|}}{{\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}$
Sử dụng phân tích
$\begin{array}{l}\overrightarrow {BE} .\overrightarrow {CF} = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right)\left( {\overrightarrow {CA} + \overrightarrow {AF} } \right)\\ = \overrightarrow {BA} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AF} + \overrightarrow {AE} .\overrightarrow {CA} + \overrightarrow {AE} .\overrightarrow {AF} \\ = 0 - \overrightarrow {AB} .\dfrac{{\overrightarrow {AB} }}{2} - \overrightarrow {AC} \dfrac{{\overrightarrow {AC} }}{2} + 0\\ = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{C^2}}}{2} = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{B^2}}}{2} = - A{B^2}.\end{array}$
$BE = CF = \sqrt {A{B^2} + A{E^2}} = \sqrt {A{B^2} + \dfrac{{A{B^2}}}{4}} = AB\sqrt {\dfrac{5}{4}} $
Từ đó suy ra $\cos a = \dfrac{{A{B^2}}}{{A{B^2}\dfrac{5}{4}}} = \dfrac{4}{5}.$
Cho ba điểm $A,B,C$ phân biệt thẳng hàng. Khi nào thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng?
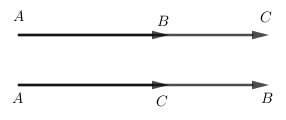
Hai véc tơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) có chung gốc \(A\) nên chúng cùng hướng nếu hai điểm \(B,C\) nằm cùng phía so với điểm \(A\) hay điểm \(A\) nằm ngoài đoạn \(BC\)
Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). Gọi \(M\) là trung điểm của \(AB\), \(N\) là điểm đối xứng với \(C\) qua $D$. Độ dài véc tơ \(\overrightarrow {MN} \) là:
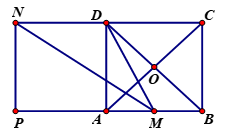
Qua $N$ kẻ đường thẳng song song với \(AD\) cắt \(AB\) tại \(P\).
Khi đó tứ giác \(ADNP\) là hình vuông và \(PM = PA + AM = a + \dfrac{a}{2} = \dfrac{{3a}}{2}\).
Áp dụng định lý Pitago trong tam giác vuông \(NPM\) ta có
\(M{N^2} = N{P^2} + P{M^2} = {a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{13{a^2}}}{4}\)\( \Rightarrow MN = \dfrac{{a\sqrt {13} }}{2}\)
Suy ra \(\left| {\overrightarrow {MN} } \right| = MN = \dfrac{{a\sqrt {13} }}{2}\).
Cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(M\) là trung điểm của \(AB\). Hãy tính độ dài của vectơ \(\overrightarrow {MD} \).
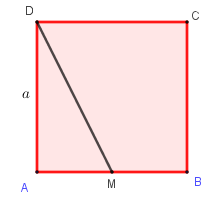
Áp dụng định lý Pitago trong tam giác vuông \(MAD\) ta có
\(D{M^2} = A{M^2} + A{D^2} = {\left( {\dfrac{a}{2}} \right)^2} + {a^2} = \dfrac{{5{a^2}}}{4}\)\( \Rightarrow DM = \dfrac{{a\sqrt 5 }}{2}\)
Suy ra \(\left| {\overrightarrow {MD} } \right| = MD = \dfrac{{a\sqrt 5 }}{2}\).
Cho tứ giác \(ABCD\). Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là đỉnh của tứ giác.
Hai điểm phân biệt, chẳng hạn \(A,\,\,B\) ta xác định được hai vectơ khác vectơ-không là \(\overrightarrow {AB} ,\,\,\overrightarrow {BA} \). Mà từ bốn đỉnh $A,\,\,B,\,\,C,\,\,D$ của tứ giác ta có $6$ cặp điểm phân biệt do đó có $12$ vectơ thỏa mãn yêu cầu bài toán.
Cho tam giác \(ABC\). Gọi \(M,\,N,\,P\) lần lượt là trung điểm của \(BC,\,CA,\,AB\). Có bao nhiêu vectơ khác vectơ - không cùng phương với \(\overrightarrow {MN} \) có điểm đầu và điểm cuối lấy trong các điểm đã cho.
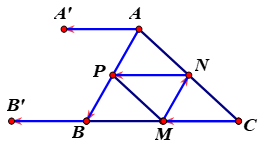
Các vectơ khác vectơ - không cùng phương với \(\overrightarrow {MN} \) là \(\overrightarrow {NM} ,\,\,\overrightarrow {AB} ,\,\,\overrightarrow {BA} ,\,\,\overrightarrow {AP} ,\,\,\overrightarrow {PA} ,\,\,\overrightarrow {BP} ,\,\,\overrightarrow {PB} \).
Cho tam giác ABC có trung tuyến AM. Chọn khẳng định đúng
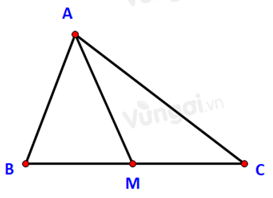
Ta có: \( \widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \( \cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
Tính giá trị của các biểu thức sau:
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \( \left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \dfrac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \dfrac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \( M = \dfrac{{\sqrt 2 }}{2}.\dfrac{{\sqrt 2 }}{2} + \dfrac{1}{2} = \dfrac{2}{4} + \dfrac{1}{2} = 1\)
Điền dấu ">,<,=" vào chỗ trống:
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
\( \Rightarrow {b^2} + {c^2} - {a^2} = 2bc\;\cos A\)(1)
Mặt khác, xét nửa đường tròn đường giác:
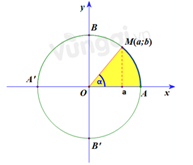
Ta có: \( \cos \alpha = a\) với a là hoành độ của điểm M.
Dễ dàng suy ra:
Nếu góc A nhọn thì \( \cos A > 0\)
Từ (1), suy ra \( {b^2} + {c^2} - {a^2} = 2bc\;\cos A > 0\)
Hay \( {b^2} + {c^2} > {a^2}\)

