Giá trị lượng giác của một góc từ 0 đến 180. Định lí côsin và định lí sin trong tam giác

Ta có $\sin {743^0} = \sin ({23^0} + {2.360^0}) = \sin 23{}^0$.

Ta có: ${a^2} = {b^2} + {c^2} - 2bc\cos A$

Ta có: \(\dfrac{a}{{\sin \,A}} = \dfrac{b}{{\sin \,B}} = \dfrac{c}{{\sin \,C}} = 2R \Rightarrow a = 2R\sin A.\)

Vì ${0^0} < x < {90^0}$ nên $\sin x > 0,\cos x > 0,\tan {\rm{ }}x > 0,\cot x > 0$

Suy ra $\cos x < 0$ sai.

    Đáp án B: $1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }},{\rm{ }}\alpha  \ne k\pi ,{\rm{ }}k \in Z$ sai vì $\cos x \ne 0{\rm{ }} \Leftrightarrow {\rm{ }}x \ne \dfrac{\pi }{2} + k\pi ,{\rm{ }}k \in Z$

    Đáp án C: ${\sin ^2}\alpha  + {\cos ^2}\beta  = 1$ sai vì \(\alpha  \ne \beta \).

    Đáp án D: $1 + {\cot ^2}\alpha  = \dfrac{1}{{{{\sin }^2}\alpha }},{\rm{ }}\alpha  \ne \dfrac{\pi }{2}{\rm{ + k}}\pi {\rm{, k}} \in Z$ sai vì $\sin x \ne 0{\rm{ }} \Leftrightarrow {\rm{ }}x \ne k\pi ,{\rm{ }}k \in Z$

$P = m\sin {0^0} + {\rm{ }}n\cos {0^0}{\rm{ }} + {\rm{ }}p\sin {90^0} = {\rm{ }}m.0{\rm{ }} + {\rm{ }}n.1{\rm{ }} + {\rm{ }}p.1{\rm{ }} = n{\rm{ }} + {\rm{ }}p$.

${\rm{S}} = {\cos ^2}{12^0} + {\cos ^2}{78^0} + {\cos ^2}{1^0} + {\cos ^2}{89^0}$

${\rm{    = (si}}{{\rm{n}}^2}{78^0} + {\cos ^2}{78^0}) + ({\sin ^2}{89^0} + {\cos ^2}{89^0})$

${\rm{    = 1 + 1 = 2}}$

$S = 3 - {\sin ^2}{90^0} + 2{\cos ^2}{60^0} - 3{\tan ^2}{45^0} = 3 - {1^2} + 2.{\left( {\dfrac{1}{2}} \right)^2} - {3.1^2} = \dfrac{{ - 1}}{2}$.

${\rm{S}} = \cos {\rm{(9}}{{\rm{0}}^0} - x)\sin \left( {{{180}^0} - x} \right)$ $ - {\rm{\sin(9}}{{\rm{0}}^0} - x)\cos \left( {{{180}^0} - x} \right)$

$\begin{array}{l}{\rm{    = sinx}}.\sin {\rm{x}} - \cos {\rm{x}}{\rm{.}}\left( { - \cos x} \right)\\{\rm{    = si}}{{\rm{n}}^2}x + {\cos ^2}x\\{\rm{  }} = 1\end{array}$

\(\dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} \Rightarrow b = \dfrac{c}{{\sin C}}.\sin B = \dfrac{5}{{\sin {{45}^0}}}.\sin {60^0} = \dfrac{{5\sqrt 6 }}{2}.\)

$\sin {120^0} = \dfrac{{\sqrt 3 }}{2} \Rightarrow {\cos ^2}{120^0} = 1 - {\sin ^2}{120^0} \Rightarrow {\cos ^2}{120^0} = \dfrac{1}{4}$

Vì ${90^0} < {120^0} < {180^0} \Rightarrow \cos {120^0} < 0 \Rightarrow \cos {120^0} = \dfrac{{ - 1}}{2}$.

Sai ở bước (IV).

$\sin {225^0} = \sin ({180^0} + {45^0}) $ $=  - \sin {45^0} = \dfrac{{ - \sqrt 2 }}{2}$

 A đúng

${\rm{\cos 22}}{{\rm{5}}^0} = \cos {\rm{(18}}{{\rm{0}}^0} + {45^0}) $ $=  - \cos {\rm{4}}{{\rm{5}}^0} =  - \dfrac{{\sqrt 2 }}{2}$

B đúng

$\tan {225^0} = \tan ({180^0} + {45^0}) = \tan {45^0} = 1$

C sai

$\cot {225^0} = \cot ({180^0} + {45^0}) = \cot {45^0} = 1$

D đúng

$\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\ = {10^2} + {16^2} - 2.10.16.\cos {60^0}\\ = {\rm{ }}196\end{array}$ .

Suy ra \(BC = a = \sqrt {196}  = 14\).

$P = 3{\sin ^2}x + 4{\cos ^2}x = 3({\sin ^2}x + {\cos ^2}x) + {\cos ^2}x = 3 + {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{{13}}{4}$.

\(\begin{array}{l}A = \dfrac{{\sin ( - {{234}^0}) - \cos {{216}^0}}}{{\sin {{144}^0} - \cos {{126}^0}}}.\tan {36^0}\\{\rm{   }} = \dfrac{{ - \sin {\rm{(18}}{{\rm{0}}^{\rm{0}}} + {{54}^0}) - \cos ({{180}^0} + {{36}^0})}}{{\sin ({{180}^0} - {{36}^0}) - \cos ({{180}^0} - {{54}^0})}}.\tan {36^0}\\{\rm{   }} = \dfrac{{{\rm{sin5}}{{\rm{4}}^{\rm{0}}} + \cos {{36}^0}}}{{\sin {{36}^0} + \cos {{54}^0}}}.\tan {36^0}\\{\rm{   }} = \dfrac{{\cos {{36}^0} + \cos {{36}^0}}}{{\sin {{36}^0} + \sin {{36}^0}}}.\tan {36^0}\\{\rm{   }} = \cot {\rm{3}}{{\rm{6}}^{\rm{0}}}.\tan {36^0} = 1\end{array}\)

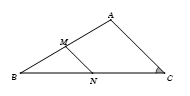
Bước 1: Tính \(AC\)

Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\).

\( \Rightarrow MN\) là đường trung bình của \(\Delta ABC\).

\( \Rightarrow MN = \dfrac{1}{2}AC\). Mà \(MN = 3\), suy ra \(AC = 6\).

Bước 2: Sử dụng định lý cô sin cho tam giác \(ABC\)

Theo định lí hàm cosin, ta có

\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\\ \Leftrightarrow {9^2} = {6^2} + B{C^2} - 2.6.BC.\cos 60^\circ \\ \Rightarrow BC = 3 + 3\sqrt 6 \end{array}\)

${\sin ^6}x + {\cos ^6}x = {({\sin ^2}x + {\cos ^2}x)^3} - 3{\sin ^2}x{\cos ^2}x({\sin ^2}x + {\cos ^2}x) = 1 - 3{\sin ^2}x{\cos ^2}x$

$\tan \alpha  + \cot \alpha  = 2 \Rightarrow {(\tan \alpha  + \cot \alpha )^2} = 4 \Rightarrow {\tan ^2}\alpha  + 2\tan \alpha \cot \alpha  + {\cot ^2}\alpha  = 4 \Rightarrow {\tan ^2}\alpha  + {\cot ^2}\alpha  = 2$

\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \cos \dfrac{{B + C}}{2} = \cos \left( {{{90}^0} - \dfrac{A}{2}} \right) = \sin \dfrac{A}{2}\)

A đúng

\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \sin \left( {A + C} \right) = \sin \left( {{{180}^0} - B} \right) = \sin B\)

B sai

\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \cos \left( {A + B + 2C} \right) = \cos \left( {{{180}^0} + C} \right) =  - \cos C\)

C đúng

\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \cos \left( {A + B} \right) = \cos \left( {{{180}^0} - C} \right) =  - \cos C\)

D đúng

Từ \(\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{BC}}{{2\sin A}} = \dfrac{{10}}{{2\sin {{30}^0}}} = 10\)