Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
- Theo định nghĩa thì \(x + y \ge 0\) là bất phương trình bậc nhất hai ẩn.
- Các bất phương trình còn lại là bất phương trình bậc hai.
Cho bất phương trình \(2x + 3y - 6 \le 0\,\,(1)\). Chọn khẳng định đúng trong các khẳng định sau
Trên mặt phẳng tọa độ, đường thẳng \(\left( d \right):2x + 3y - 6 = 0\,\,\)chia mặt phẳng thành hai nửa mặt phẳng.
Chọn điểm \(O\left( {0;0} \right)\) không thuộc đường thẳng đó. Ta thấy \(\left( {x;y} \right) = \left( {0;0} \right)\) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm của bất phương trình là nửa mặt phẳng bờ \(\left( d \right)\) chứa điểm \(O\left( {0;0} \right)\) kể cả \(\left( d \right)\).
Vậy bất phương trình $\left( 1 \right)$ luôn có vô số nghiệm.
Miền nghiệm của bất phương trình \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\) không chứa điểm:
Ta có: \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\)\( \Leftrightarrow - x + 2 + 2y - 4 < 2 - 2x\)\( \Leftrightarrow x + 2y < 4\)
Dễ thấy tại điểm \(\left( {4;\,2} \right)\) ta có: \(4 + 2.2 = 8 > 4\) nên điểm $(4;2)$ không thuộc miền nghiệm của bất phương trình.
Cho bất phương trình\( - 2x + \sqrt 3 y + \sqrt 2 \le 0\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?
Ta thấy \(\left( {\dfrac{{\sqrt 2 }}{2};0} \right) \in S\) vì \( - 2.\dfrac{{\sqrt 2 }}{2} + \sqrt 3 .0 + \sqrt 2 = 0\) nên B đúng.
Ngoài ra khi ta thay tọa độ các điểm ở đáp án A, C, D ta thấy \(\left( {1;1} \right) \notin S\), \(\left( {1; - 2} \right) \in S\) và \(\left( {1;0} \right) \in S\) nên A, C, D đều sai
Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y > - 6\) là
Trước hết, ta vẽ đường thẳng \(\left( d \right):3x - 2y = - 6.\)
Ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng có bờ là \(\left( d \right)\) chứa điểm \(\left( {0\,\,;\,\,0} \right)\) (miền nghiệm không tính cả bờ).

Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).
Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
Thay y=0 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(x + 2.0 \ge 0 \Leftrightarrow x \ge 0\)
Ta thấy bất phương trình bài cho tương đương với bất phương trình \(x \ge 0\) nên số giá trị của x thỏa mãn bất phương trình đã cho là số x thỏa mãn điều kiện \(x \ge 0\) .
Mà ta có vô số giá trị của x thỏa mãn \(x \ge 0\) nên có vô số giá trị của x thỏa mãn bất phương trình đã cho.
Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

Giả sử, từ thứ Hai đến thứ Sáu, tổng số kilômét ông An đi là x (km) và trong hai ngày cuối tuần, tổng số kilômét ông An đi là y (km). Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho
tổng số tiền ông An phải trả không quá 14 triệu đồng.
Ta có 14 triệu = $14 000$ (nghìn đồng)
Số tiền ông An đi $x$ km trong các ngày từ thứ Hai đến thứ Sáu là $8x$ (nghìn đồng)
Tổng chi phí cố định cho các ngày từ thứ Hai đến thứ Sáu là $900.5=4 500$ (nghìn đồng)
Số tiền ông An đi $y$ km trong 2 cuối tuần là $10y$ (nghìn đồng)
Tổng chi phí cố định cho 2 ngày cuối tuần là $1500.2=3000$ (nghìn đồng)
Tổng số tiền ông An đi trong một tuần là $8x+10y+4500+3000$ (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x +4500+ 10y +3000\le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\).
Cặp số nào sau đây là nghiệm của bất phương trình \(2x - 3y < 3\)?
\(\left( {2;1} \right)\)
\(\left( {2;1} \right)\)
\(\left( {2;1} \right)\)
+ Thay \(x = 0,y = - 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.0 - 3.\left( { - 1} \right) < 3 \Leftrightarrow 3 < 3\) (Vô lý)
Vậy \(\left( {0; - 1} \right)\) không là nghiệm.
+ Thay \(x = 2,y = 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.2 - 3.1 < 3 \Leftrightarrow 1 < 3\) (Luôn đúng)
Vậy \(\left( {2;1} \right)\) là nghiệm.
+ Thay \(x = 3,y = 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.3 - 3.1 < 3 \Leftrightarrow 3 < 3\) (Vô lý)
Vậy \(\left( {3;1} \right)\) không là nghiệm.
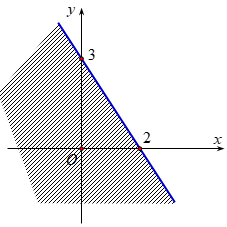
Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Đường thẳng qua điểm (2;0) và (0;1) nên phương trình đường thẳng là
Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)
Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)
=> \(a = - \dfrac{1}{2},b = 1\)
=> phương trình đường thẳng là \(y = - \dfrac{1}{2}x + 1\)
Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \dfrac{1}{2}x + 1 - y = \dfrac{{ - 1}}{2} < 0\)
=> Bất phương trình cần tìm là \( - \dfrac{1}{2}x - y + 1 < 0\)